Conditional quantum entropy
Encyclopedia
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy
of classical information theory. The conditional entropy is written
, or 
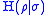, depending on the notation being used for the von Neumann entropy
.
For the remainder of the article, we use the notation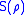
for the von Neumann entropy.
and 
, the von Neumann entropies are 
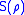and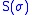 
. The von Neumann entropy measures how uncertain we are about the value of the state; how much the state is a mixed state. The joint quantum entropy
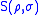measures our uncertainty about the joint system which contains both states.
By analogy with the classical conditional entropy, one defines the conditional quantum entropy as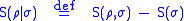
.
An equivalent (and more intuitive) operational definition of the quantum conditional entropy (as a measure of the quantum communication cost or surplus when performing quantum state merging) was given by Michał Horodecki, Jonathan Oppenheim
, and Andreas Winter
in their paper "Quantum Information can be negative" http://arxiv.org/abs/quant-ph/0505062.
, the conditional quantum entropy can be negative. This is true even though the (quantum) von Neumann entropy of single variable is never negative.
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
of classical information theory. The conditional entropy is written
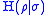, or , depending on the notation being used for the von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
.
For the remainder of the article, we use the notation
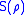for the von Neumann entropy.Definition
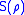Given two quantum states and , the von Neumann entropies are and 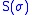. The von Neumann entropy measures how uncertain we are about the value of the state; how much the state is a mixed state. The joint quantum entropyJoint quantum entropy
The joint quantum entropy generalizes the classical joint entropy to the context of quantum information theory. Intuitively, given two quantum states \rho and \sigma, represented as density operators that are subparts of a quantum system, the joint quantum entropy is a measure of the total...
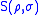measures our uncertainty about the joint system which contains both states.By analogy with the classical conditional entropy, one defines the conditional quantum entropy as
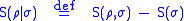.An equivalent (and more intuitive) operational definition of the quantum conditional entropy (as a measure of the quantum communication cost or surplus when performing quantum state merging) was given by Michał Horodecki, Jonathan Oppenheim
Jonathan Oppenheim
Jonathan Oppenheim is a Royal Society Research Fellow in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge. He is an expert in quantum information theory and quantum gravity. His Ph.D. under Bill Unruh at the University of British Columbia was on Quantum...
, and Andreas Winter
Andreas Winter
Andreas Winter is a mathematician at the University of Bristol and CQT at the National University of Singapore. He received his Ph.D...
in their paper "Quantum Information can be negative" http://arxiv.org/abs/quant-ph/0505062.
Properties
Unlike the classical conditional entropyConditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
, the conditional quantum entropy can be negative. This is true even though the (quantum) von Neumann entropy of single variable is never negative.