Joint quantum entropy
Encyclopedia
The joint quantum entropy generalizes the classical joint entropy to the context of quantum information theory. Intuitively, given two quantum states 
and 
, represented as density operators that are subparts of a quantum system, the joint quantum entropy is a measure of the total uncertainty or entropy
of the joint system. It is written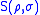
or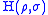 
, depending on the notation being used for the von Neumann entropy
. Like other entropies, the joint quantum entropy is measured in bit
s, i.e. the logarithm is taken in base 2.
In this article, we will use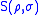
for the joint quantum entropy.
, for any classical random variable
, the classical Shannon entropy 
is a measure of how uncertain we are about the outcome of 
. For example, if 
is a probability distribution concentrated at one point, the outcome of 
is certain and therefore its entropy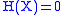 
. At the other extreme, if 
is the uniform probability distribution with 
possible values, intuitively one would expect 
is associated with the most uncertainty. Indeed such uniform probability distributions have maximum possible entropy 
.
In quantum information theory, the notion of entropy is extended from probability distributions to quantum states, or density matrices
. For a state
, the von Neumann entropy
is defined by
Applying the spectral theorem
, or Borel functional calculus
for infinite dimensional systems, we see that it generalizes the classical entropy. The physical meaning remains the same. A maximally mixed state, the quantum analog of the uniform probability distribution, has maximum von Neumann entropy. On the other hand, a pure state, or a rank one projection, will have zero von Neumann entropy. We write the von Neumann entropy
(or sometimes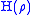 
.
In symbols, if the combined system is in state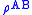
,
the joint quantum entropy is then
Each subsystem has it own entropy. The state of the subsystems are given by the partial trace
operation.
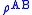exhibits quantum entanglement
, then the entropy of each subsystem may be larger than the joint entropy. This is equivalent to the fact that the conditional quantum entropy may be negative, while the classical conditional entropy may never be.
Consider a maximally entangled state such as a Bell state
. If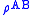
is a Bell state, say,
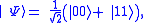
then the total system is a pure state, with entropy 0, while each individual subsystem is a maximally mixed state, with maximum von Neumann entropy
. Thus the joint entropy of the combined system is less than that of subsystems. This is because for entangled states, definite states cannot be assigned to subsystems, resulting in positive entropy.
Notice that the above phenomenon cannot occur if a state is a separable pure state. In that case, the reduced states of the subsystems are also pure. Therefore all entropies are zero.
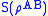can be used to define of the conditional quantum entropy
:
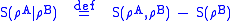
and the quantum mutual information
:
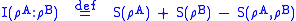
These definitions parallel the use of the classical joint entropy to define the conditional entropy
and mutual information
.
and , represented as density operators that are subparts of a quantum system, the joint quantum entropy is a measure of the total uncertainty or entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the joint system. It is written
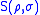or 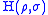, depending on the notation being used for the von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
. Like other entropies, the joint quantum entropy is measured in bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s, i.e. the logarithm is taken in base 2.
In this article, we will use
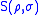for the joint quantum entropy.Background
In information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, for any classical random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, the classical Shannon entropy is a measure of how uncertain we are about the outcome of . For example, if is a probability distribution concentrated at one point, the outcome of is certain and therefore its entropy 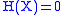. At the other extreme, if is the uniform probability distribution with possible values, intuitively one would expect is associated with the most uncertainty. Indeed such uniform probability distributions have maximum possible entropy .In quantum information theory, the notion of entropy is extended from probability distributions to quantum states, or density matrices
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
. For a state
, the von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
is defined by
Applying the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, or Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
for infinite dimensional systems, we see that it generalizes the classical entropy. The physical meaning remains the same. A maximally mixed state, the quantum analog of the uniform probability distribution, has maximum von Neumann entropy. On the other hand, a pure state, or a rank one projection, will have zero von Neumann entropy. We write the von Neumann entropy
(or sometimes 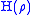.Definition
Given a quantum system with two subsystems A and B, the term joint quantum entropy simply refers to the von Neumann entropy of the combined system. This is to distinguish from the entropy of the subsystems.In symbols, if the combined system is in state
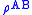,the joint quantum entropy is then
Each subsystem has it own entropy. The state of the subsystems are given by the partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
operation.
Properties
The classical joint entropy is always at least equal to the entropy of each individual system. This is not the case for the joint quantum entropy. If the quantum state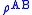 exhibits quantum entanglementQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, then the entropy of each subsystem may be larger than the joint entropy. This is equivalent to the fact that the conditional quantum entropy may be negative, while the classical conditional entropy may never be.
Consider a maximally entangled state such as a Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
. If
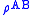is a Bell state, say,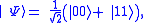then the total system is a pure state, with entropy 0, while each individual subsystem is a maximally mixed state, with maximum von Neumann entropy
. Thus the joint entropy of the combined system is less than that of subsystems. This is because for entangled states, definite states cannot be assigned to subsystems, resulting in positive entropy.Notice that the above phenomenon cannot occur if a state is a separable pure state. In that case, the reduced states of the subsystems are also pure. Therefore all entropies are zero.
Relations to other entropy measures
The joint quantum entropy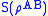 can be used to define of the conditional quantum entropyConditional quantum entropy
The conditional quantum entropy is an entropy measure used in quantum information theory. It is a generalization of the conditional entropy of classical information theory...
:
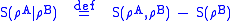
and the quantum mutual information
Quantum mutual information
In quantum information theory, quantum mutual information, or von Neumann mutual information, after John von Neumann, is a measure of correlation between subsystems of quantum state...
:
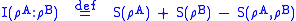
These definitions parallel the use of the classical joint entropy to define the conditional entropy
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
and mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
.