
Statistical model validation
Encyclopedia
In statistics
, model validation is possibly the most important step in the model
building sequence. It is also one of the most overlooked. Often the validation of a model seems to consist of nothing more than quoting the R2 statistic from the fit (which measures the fraction of the total variability
in the response that is accounted for by the model).
) value does not guarantee that the model fits the data well. Use of a model that does not fit the data well cannot provide good answers to the underlying engineering or scientific questions under investigation.
However to increase the precision of the R2, some statisticians suggest that you should use the adjusted R2 to reflect both the number of independent variables in the model and sample size. This is only useful for multiple regression.
from a fitted model are the differences between the responses observed at each combination values of the explanatory variables and the corresponding prediction of the response computed using the regression function. Mathematically, the definition of the residual for the ith observation in the data set
is written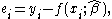
with yi denoting the ith response in the data set and xi the vector of explanatory variables, each set at the corresponding values found in the ith observation in the data set.
If the model fit to the data were correct, the residuals would approximate the random errors that make the relationship between the explanatory variables and the response variable a statistical relationship. Therefore, if the residuals appear to behave randomly, it suggests that the model fits the data well. On the other hand, if non-random structure is evident in the residuals, it is a clear sign that the model fits the data poorly. The next section details the types of plots to use to test different aspects of a model and give guidance on the correct interpretations of different results that could be observed for each type of plot.
Graphical methods have an advantage over numerical methods for model validation because they readily illustrate a broad range of complex aspects of the relationship between the model and the data.
for assessing the correctness of the functional part of the model can aid in interpreting a borderline residual plot. There are also a few modeling situations in which graphical methods cannot easily be used. In these cases, numerical methods provide a fallback position for model validation. One common situation when numerical validation methods take precedence over graphical methods is when the number of parameters
being estimated is relatively close to the size of the data set. In this situation residual plots are often difficult to interpret due to constraints on the residuals imposed by the estimation of the unknown parameters. One area in which this typically happens is in optimization applications using designed experiments. Logistic regression
with binary data is another area in which graphical residual analysis can be difficult.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, model validation is possibly the most important step in the model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
building sequence. It is also one of the most overlooked. Often the validation of a model seems to consist of nothing more than quoting the R2 statistic from the fit (which measures the fraction of the total variability
Variability
The term variability, "the state or characteristic of being variable", describes how spread out or closely clustered a set of data is. This may be applied to many different subjects:*Climate variability...
in the response that is accounted for by the model).
R2 is not enough
Unfortunately, a high R2 (coefficient of determinationCoefficient of determination
In statistics, the coefficient of determination R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model...
) value does not guarantee that the model fits the data well. Use of a model that does not fit the data well cannot provide good answers to the underlying engineering or scientific questions under investigation.
However to increase the precision of the R2, some statisticians suggest that you should use the adjusted R2 to reflect both the number of independent variables in the model and sample size. This is only useful for multiple regression.
Analysis of residuals
The residualsErrors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
from a fitted model are the differences between the responses observed at each combination values of the explanatory variables and the corresponding prediction of the response computed using the regression function. Mathematically, the definition of the residual for the ith observation in the data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
is written
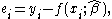
with yi denoting the ith response in the data set and xi the vector of explanatory variables, each set at the corresponding values found in the ith observation in the data set.
If the model fit to the data were correct, the residuals would approximate the random errors that make the relationship between the explanatory variables and the response variable a statistical relationship. Therefore, if the residuals appear to behave randomly, it suggests that the model fits the data well. On the other hand, if non-random structure is evident in the residuals, it is a clear sign that the model fits the data poorly. The next section details the types of plots to use to test different aspects of a model and give guidance on the correct interpretations of different results that could be observed for each type of plot.
Graphical analysis of residuals
There are many statistical tools for model validation, but the primary tool for most modeling applications is graphical residual analysis. Different types of plots of the residuals from a fitted model provide information on the adequacy of different aspects of the model.- sufficiency of the functional part of the model: scatter plots of residuals versus predictors
- non-constant variation across the data: scatter plots of residuals versus predictors; for data collected over time, also plots of residuals against time
- drift in the errors (data collected over time): run chartRun ChartA run chart, also known as a run-sequence plot is a graph that displays observed data in a time sequence. Often, the data displayed represent some aspect of the output or performance of a manufacturing or other business process.- Overview :...
s of the response and errors versus time - independence of errors: lag plot
- normality of errors: histogramHistogramIn statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
and normal probability plotNormal probability plotThe normal probability plot is a graphical technique for normality testing: assessing whether or not a data set is approximately normally distributed....
Graphical methods have an advantage over numerical methods for model validation because they readily illustrate a broad range of complex aspects of the relationship between the model and the data.
Quantitative analysis of residuals
Numerical methods for model validation, such as the R2 statistic, are also useful, but usually to a lesser degree than graphical methods. Numerical methods for model validation tend to be narrowly focused on a particular aspect of the relationship between the model and the data and often try to compress that information into a single descriptive number or test result. Numerical methods do play an important role as confirmatory methods for graphical techniques, however. For example, the lack-of-fit testLack-of-fit test
In statistics, a lack-of-fit test is any of many tests of a null hypothesis that a proposed statistical model fits well. See:* Goodness of fit* Lack-of-fit sum of squares...
for assessing the correctness of the functional part of the model can aid in interpreting a borderline residual plot. There are also a few modeling situations in which graphical methods cannot easily be used. In these cases, numerical methods provide a fallback position for model validation. One common situation when numerical validation methods take precedence over graphical methods is when the number of parameters
Statistical parameter
A statistical parameter is a parameter that indexes a family of probability distributions. It can be regarded as a numerical characteristic of a population or a model....
being estimated is relatively close to the size of the data set. In this situation residual plots are often difficult to interpret due to constraints on the residuals imposed by the estimation of the unknown parameters. One area in which this typically happens is in optimization applications using designed experiments. Logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
with binary data is another area in which graphical residual analysis can be difficult.

