Steinberg group (K-theory)
Encyclopedia
In algebraic K-theory
, a field of mathematics
, the Steinberg group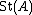
of a ring A, is the universal central extension of the commutator subgroup
of the stable general linear group
.
It is named after Robert Steinberg
, and is connected with lower K-groups, notably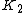
and 
.
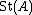is the universal central extension of the commutator subgroup
of the stable general linear group
(the commutator subgroup is perfect, hence has a universal central extension).
Concretely, it can also be described by generators and relations.
, where 
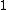is the identity matrix, 
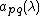is the matrix with 
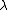in the 
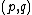entry and zeros elsewhere, and 
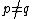—satisfy the following relations, called the Steinberg relations:
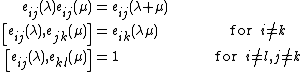
The unstable Steinberg group of order r over A,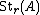
, is defined by the generators
, 
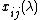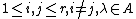, subject to the Steinberg relations. The stable Steinberg group, 
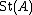, is the direct limit
of the system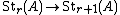
. It can also be thought of as the Steinberg group of infinite order.
Mapping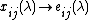
yields a group homomorphism
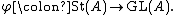
As the elementary matrices generate the commutator subgroup
, this map is onto the commutator subgroup.
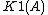is the cokernel
of the map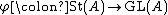
, as 
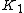is the abelianization of 
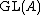and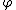 
is onto the commutator subgroup.
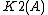is the center of the Steinberg group; this was Milnor's definition, and also follows from more general definitions of higher K-groups.
It is also the kernel
of the map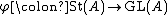
, and indeed there is an exact sequence
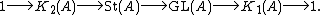
Equivalently, it is the Schur multiplier
of the group of elementary matrices, and thus is also a homology group: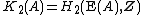
.
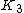of a ring is 
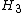of the Steinberg group.
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, a field of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Steinberg group
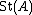of a ring A, is the universal central extension of the commutator subgroupCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the stable general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
.
It is named after Robert Steinberg
Robert Steinberg
Robert Steinberg is a mathematician at the University of California, Los Angeles who invented the Steinberg representation, the Steinberg group in algebraic K-theory, and the Steinberg groups in Lie theory that yield finite simple groups over finite fields. He received his Ph.D...
, and is connected with lower K-groups, notably
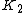and .Definition
Abstractly, given a ring A, the Steinberg group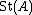 is the universal central extension of the commutator subgroupCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the stable general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
(the commutator subgroup is perfect, hence has a universal central extension).
Concretely, it can also be described by generators and relations.
Steinberg relations
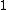Elementary matrices—meaning matrices of the form, where is the identity matrix, 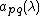is the matrix with 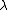in the 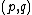entry and zeros elsewhere, and 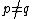—satisfy the following relations, called the Steinberg relations: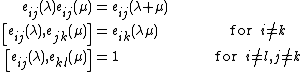The unstable Steinberg group of order r over A,
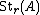, is defined by the generators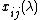, , 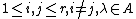subject to the Steinberg relations. The stable Steinberg group, 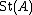, is the direct limitDirect limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the system
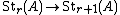. It can also be thought of as the Steinberg group of infinite order.Mapping
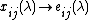yields a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
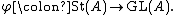
As the elementary matrices generate the commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
, this map is onto the commutator subgroup.
K1
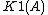is the cokernelCokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of the map
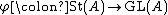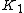, as is the abelianization of 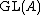and 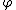is onto the commutator subgroup.K2
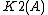is the center of the Steinberg group; this was Milnor's definition, and also follows from more general definitions of higher K-groups.It is also the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the map
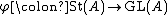, and indeed there is an exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
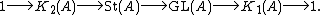
Equivalently, it is the Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
of the group of elementary matrices, and thus is also a homology group:
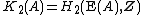.K3
showed that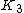 of a ring is 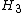of the Steinberg group.