
Steinitz exchange lemma
Encyclopedia
The Steinitz exchange lemma is a basic theorem in linear algebra
used, for example, to show that any two bases
for a finite-dimensional
vector space
have the same number of elements. The result is named after the German mathematician Ernst Steinitz
. The result is often called the Steinitz–Mac Lane exchange lemma, also recognizing the generalization
by Saunders Mac Lane
of Steinitz's lemma to matroid
s.
vectors in a vector space V, and {w1, ..., wn} span
V then m ≤ n and, possibly after reordering the wi, the set {v1, ..., vm, wm + 1, ..., wn} spans V.
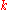 satisfying
satisfying  , the following assertion is valid:
, the following assertion is valid:
(1) we have , and the set
, and the set 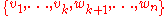 spans
spans  .
.
In fact, we will prove (1) by induction over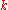 : Being clear for
: Being clear for  , the only thing that needs to be done is the induction step. So assume that some
, the only thing that needs to be done is the induction step. So assume that some 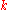 satisfying
satisfying  is such that
is such that  and such that the set
and such that the set 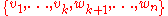 spans
spans  . Then,
. Then,  (because otherwise, we would have
(because otherwise, we would have  , so that the set
, so that the set 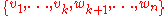 would be equal to the set
would be equal to the set  , but this set cannot span
, but this set cannot span  since
since  and since the set
and since the set  is linearly independent), and thus
is linearly independent), and thus  can be sharpened to
can be sharpened to 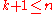 .
.
Since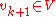 , we may write
, we may write 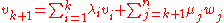 . As also
. As also  are linearly independent not all the
are linearly independent not all the 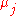 may be zero. Thus without loss of generality, by reordering the
may be zero. Thus without loss of generality, by reordering the  , we may assume that
, we may assume that  is not zero. Therefore, the equation
is not zero. Therefore, the equation 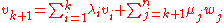 can be used to write
can be used to write  as a linear combination of
as a linear combination of  . In other words,
. In other words,  is in the span of
is in the span of  and so the latter must be the whole of
and so the latter must be the whole of  . This completes the induction step, and (1) follows by induction on
. This completes the induction step, and (1) follows by induction on 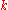 . The Lemma now follows from (1), applied to
. The Lemma now follows from (1), applied to  .
.
, especially in linear algebra
and in combinatorial algorithms.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
used, for example, to show that any two bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for a finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
have the same number of elements. The result is named after the German mathematician Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
. The result is often called the Steinitz–Mac Lane exchange lemma, also recognizing the generalization
by Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
of Steinitz's lemma to matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s.
Statement
If {v1, ..., vm} is a set of m linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
vectors in a vector space V, and {w1, ..., wn} span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
V then m ≤ n and, possibly after reordering the wi, the set {v1, ..., vm, wm + 1, ..., wn} spans V.
Proof
We are going to show that for any integer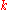 satisfying
satisfying  , the following assertion is valid:
, the following assertion is valid:(1) we have
 , and the set
, and the set 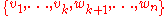 spans
spans  .
.In fact, we will prove (1) by induction over
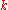 : Being clear for
: Being clear for  , the only thing that needs to be done is the induction step. So assume that some
, the only thing that needs to be done is the induction step. So assume that some 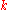 satisfying
satisfying  is such that
is such that  and such that the set
and such that the set 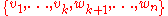 spans
spans  . Then,
. Then,  (because otherwise, we would have
(because otherwise, we would have  , so that the set
, so that the set 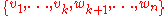 would be equal to the set
would be equal to the set  , but this set cannot span
, but this set cannot span  since
since  and since the set
and since the set  is linearly independent), and thus
is linearly independent), and thus  can be sharpened to
can be sharpened to 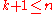 .
.Since
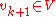 , we may write
, we may write 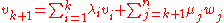 . As also
. As also  are linearly independent not all the
are linearly independent not all the 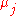 may be zero. Thus without loss of generality, by reordering the
may be zero. Thus without loss of generality, by reordering the  , we may assume that
, we may assume that  is not zero. Therefore, the equation
is not zero. Therefore, the equation 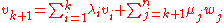 can be used to write
can be used to write  as a linear combination of
as a linear combination of  . In other words,
. In other words,  is in the span of
is in the span of  and so the latter must be the whole of
and so the latter must be the whole of  . This completes the induction step, and (1) follows by induction on
. This completes the induction step, and (1) follows by induction on 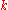 . The Lemma now follows from (1), applied to
. The Lemma now follows from (1), applied to  .
.Applications
The Steinitz exchange lemma is a basic result in computational mathematicsComputational mathematics
Computational mathematics involves mathematical research in areas of science where computing plays a central and essential role, emphasizing algorithms, numerical methods, and symbolic methods. Computation in the research is prominent. Computational mathematics emerged as a distinct part of applied...
, especially in linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
and in combinatorial algorithms.

