The Stokes number, named after Irish

 mathematician George Gabriel Stokes

George Gabriel Stokes

Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...

, is a dimensionless number corresponding to the behavior of particles suspended

Suspension (chemistry)

In chemistry, a suspension is a heterogeneous fluid containing solid particles that are sufficiently large for sedimentation. Usually they must be larger than 1 micrometer. The internal phase is dispersed throughout the external phase through mechanical agitation, with the use of certain...

 in a fluid flow. Stokes number is defined as the ratio of the stopping distance of a particle to a characteristic dimension of the obstacle, or

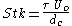
where is the relaxation time

Relaxation time

In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium.Each relaxation process can be characterized by a relaxation time τ...

 of the particle, is the fluid velocity of the flow well away from the obstacle and 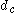is the characteristic dimension of the obstacle.

In experimental fluid dynamics, the Stokes number (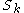) is a measure of flow tracer fidelity in particle image velocimetry (PIV)

Particle image velocimetry

Particle image velocimetry is an optical method of flow visualization used in education and research. It is used to obtain instantaneous velocity measurements and related properties in fluids...

 experiments where very small particles are entrained in turbulent flows and optically observed to determine the speed and direction of fluid movement (also known as the velocity field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

of the fluid). For acceptable tracing accuracy, the particle response time should be faster than the smallest time scale of the flow. Smaller Stokes numbers represent better tracing accuracy; for 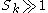, particles will detach from a flow especially where the flow decelerates abruptly. For 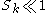, particles follow fluid streamlines closely. If 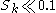, tracing accuracy errors are below 1%.

Application to anisokinetic sampling of particles

For example, the selective capture of particles by an aligned, thin-walled circular nozzle is given by Belyaev and Levin as: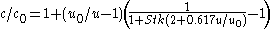

where is particle concentration, is speed, and the subscript 0 indicates conditions far upstream of the nozzle. The characteristic distance is the diameter of the nozzle. Here the Stokes number is calculated,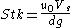

where 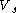is the particle's settling velocity, 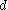is the sampling tubes inner diameter, and 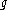is the acceleration of gravity.

External links

• Reynolds number scaling of particle clustering in turbulent aerosols