Stress measures
Encyclopedia
The most commonly used measure of stress is the Cauchy stress
. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:
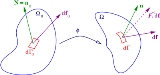
In the reference configuration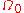 , the outward normal to a surface element
, the outward normal to a surface element 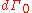 is
is  and the traction acting on that surface is
and the traction acting on that surface is  leading to a force vector
leading to a force vector 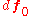 . In the deformed configuration
. In the deformed configuration  , the surface element changes to
, the surface element changes to  with outward normal
with outward normal  and traction vector
and traction vector  leading to a force
leading to a force 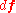 . Note that this surface can either be a hypothetical cut inside the body or an actual surface.
. Note that this surface can either be a hypothetical cut inside the body or an actual surface.

or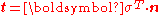
where is the traction and
is the traction and  is the normal to the surface on which the traction acts.
is the normal to the surface on which the traction acts.
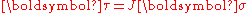 is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is no change in volume during plastic deformation).
 is the transpose of the first Piola-Kirchhoff stress (PK1 stress)
is the transpose of the first Piola-Kirchhoff stress (PK1 stress) 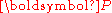 and is defined via
and is defined via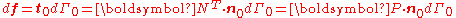
or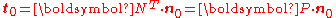
This stress is unsymmetric and is a two point tensor like the deformation gradient. This is because it relates the force in the deformed configuration to an oriented area vector in the reference configuration.
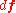 to the reference configuration, we have
to the reference configuration, we have
or,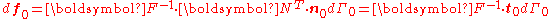
The PK2 stress (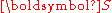 ) is symmetric and is defined via the relation
) is symmetric and is defined via the relation
Therefore,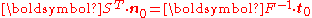
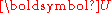 . The Biot stress is defined as the symmetric part of the tensor
. The Biot stress is defined as the symmetric part of the tensor 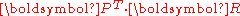 where
where 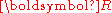 is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore the Biot stress tensor is defined as
is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore the Biot stress tensor is defined as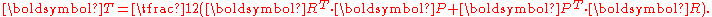
The Biot stress is also called the Jaumann stress.
The quantity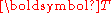 does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation
does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation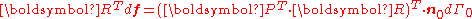

Now,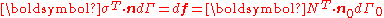
Hence,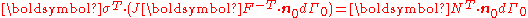
or,
or,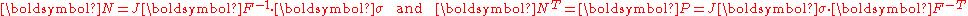
In index notation,
Therefore,
Note that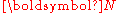 and
and  are not symmetric because
are not symmetric because 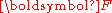 is not symmetric.
is not symmetric.
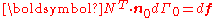
and
Therefore,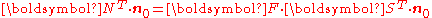
or (using the symmetry of ),
),
In index notation,
Alternatively, we can write
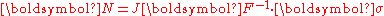
In terms of the 2nd PK stress, we have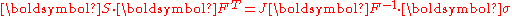
Therefore,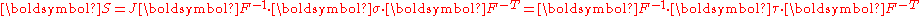
In index notation,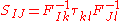
Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2n PK stress is also symmetric.
Alternatively, we can write
or,
Clearly, from definition of the push-forward and pull-back operations, we have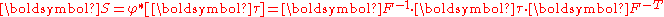
and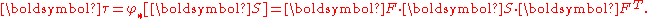
Therefore, is the pull back of
is the pull back of  by
by 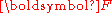 and
and  is the push forward of
is the push forward of  .
.
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:
- The Cauchy stress (
 ) or true stress.
) or true stress. - The Kirchhoff stress (
 ).
). - The Nominal stress (
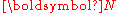 ).
). - The first Piola-Kirchhoff stress (
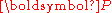 ). This stress tensor is the transpose of the nominal stress (
). This stress tensor is the transpose of the nominal stress (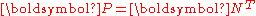 ).
). - The second Piola-Kirchhoff stress or PK2 stress (
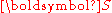 ).
). - The Biot stress (
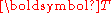 )
)
Definitions of stress measures
Consider the situation shown the following figure. The following definitions use the notations shown in the figure. |
In the reference configuration
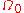 , the outward normal to a surface element
, the outward normal to a surface element 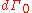 is
is  and the traction acting on that surface is
and the traction acting on that surface is  leading to a force vector
leading to a force vector 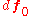 . In the deformed configuration
. In the deformed configuration  , the surface element changes to
, the surface element changes to  with outward normal
with outward normal  and traction vector
and traction vector  leading to a force
leading to a force 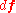 . Note that this surface can either be a hypothetical cut inside the body or an actual surface.
. Note that this surface can either be a hypothetical cut inside the body or an actual surface.Cauchy stress
The Cauchy stress (or true stress) is a measure of the force acting on an element of area in the deformed configuration. This tensor is symmetric and is defined via
or
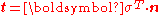
where
 is the traction and
is the traction and  is the normal to the surface on which the traction acts.
is the normal to the surface on which the traction acts.Kirchhoff stress
The quantity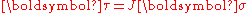 is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where thereis no change in volume during plastic deformation).
Nominal stress/First Piola-Kirchhoff stress
The nominal stress is the transpose of the first Piola-Kirchhoff stress (PK1 stress)
is the transpose of the first Piola-Kirchhoff stress (PK1 stress) 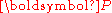 and is defined via
and is defined via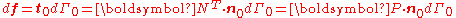
or
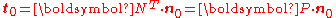
This stress is unsymmetric and is a two point tensor like the deformation gradient. This is because it relates the force in the deformed configuration to an oriented area vector in the reference configuration.
Second Piola-Kirchhoff stress
If we pull back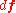 to the reference configuration, we have
to the reference configuration, we have
or,
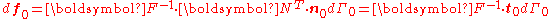
The PK2 stress (
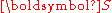 ) is symmetric and is defined via the relation
) is symmetric and is defined via the relation
Therefore,
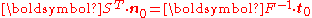
Biot stress
The Biot stress is useful because it is energy conjugate to the right stretch tensor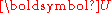 . The Biot stress is defined as the symmetric part of the tensor
. The Biot stress is defined as the symmetric part of the tensor 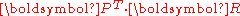 where
where 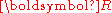 is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore the Biot stress tensor is defined as
is the rotation tensor obtained from a polar decomposition of the deformation gradient. Therefore the Biot stress tensor is defined as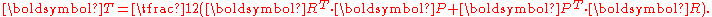
The Biot stress is also called the Jaumann stress.
The quantity
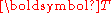 does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation
does not have any physical interpretation. However, the unsymmetrized Biot stress has the interpretation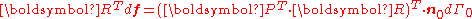
Relations between Cauchy stress and nominal stress
From Nanson's formula relating areas in the reference and deformed configurations:
Now,
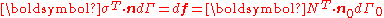
Hence,
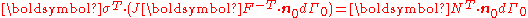
or,

or,
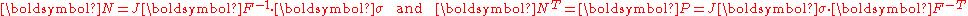
In index notation,

Therefore,

Note that
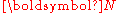 and
and  are not symmetric because
are not symmetric because 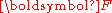 is not symmetric.
is not symmetric.Relations between nominal stress and second P-K stress
Recall that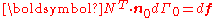
and

Therefore,
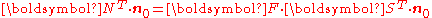
or (using the symmetry of
 ),
),
In index notation,

Alternatively, we can write

Relations between Cauchy stress and second P-K stress
Recall that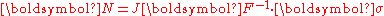
In terms of the 2nd PK stress, we have
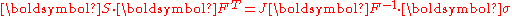
Therefore,
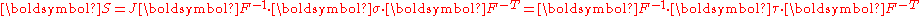
In index notation,
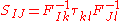
Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2n PK stress is also symmetric.
Alternatively, we can write

or,

Clearly, from definition of the push-forward and pull-back operations, we have
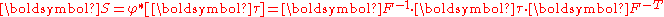
and
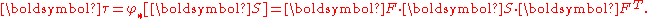
Therefore,
 is the pull back of
is the pull back of  by
by 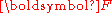 and
and  is the push forward of
is the push forward of  .
.See also
- Stress (physics)Stress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- Finite strain theory
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Cauchy elastic materialCauchy elastic materialA Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation . A Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation (with respect to an...

