Cauchy elastic material
Encyclopedia
A Cauchy-elastic material is one in which the Cauchy stress
at each material point is determined only by the current state of deformation (with respect to an arbitrary reference configuration). (Typically, the reference configuration is taken as the undeformed configuration. However, it is not the only choice for the reference configuration.) Therefore, the Cauchy stress in such a material does not depend on the path of deformation or the history of deformation. Neither does the stress depend on the time taken to achieve that deformation or the rate at which the state of deformation is reached. A Cauchy elastic material is also called a simple elastic material.
Unlike in a hyperelastic material
(which is sometimes referred to as Green elastic material), the work done by stresses does depend on the path of deformation. Therefore a Cauchy elastic material has a non-conservative structure and the stress cannot be derived from a scalar potential function.
A Cauchy elastic material must satisfy the requirements of material objectivity
and the principle of local action, i.e., the constitutive equation
s are spatially local. This assumption excludes action at a distance from being present in a constitutive relation (no nonlocal materials allowed). Also it enforces the requirement that body forces, such as gravity, and inertial forces cannot affect the properties of the material.
Though a Cauchy elastic material is a mathematical idealization of elastic material behavior, this description applies to many of the purely mechanical constitutive relations for elastic materials found in nature.
for the Cauchy stress tensor
can be formulated based on the deformation gradient: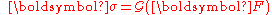
where
is the Cauchy stress and 
is the deformation gradient. Note that the function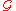 
depends on the choice of reference configuration.
Frame indifference
requires that the constitutive relation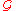
should not change when the location of the observer changes. Therefore the constitutive equation
for another arbitrary observer can be written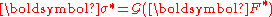
. Knowing that the Cauchy stress tensor
and the deformation gradient 
are objective quantities, one can write:
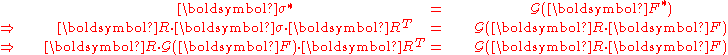
where
is a proper orthogonal tensor.
The above is a condition that the constitutive law
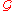has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive laws
relating the deformation gradient to the first or second Piola-Kirchhoff stress tensor.
can be expressed as a function of the left Cauchy-Green tensor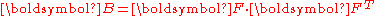 
. The constitutive equation
may then be written:
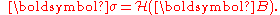
In order to find the restriction on
which will ensure the principle of material frame-indifference, one can write:
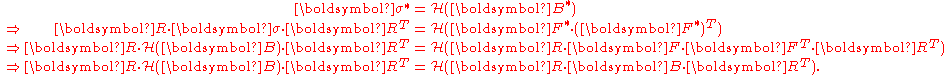
A constitutive equation
that respects the above condition is said to be isotropic.
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
at each material point is determined only by the current state of deformation (with respect to an arbitrary reference configuration). (Typically, the reference configuration is taken as the undeformed configuration. However, it is not the only choice for the reference configuration.) Therefore, the Cauchy stress in such a material does not depend on the path of deformation or the history of deformation. Neither does the stress depend on the time taken to achieve that deformation or the rate at which the state of deformation is reached. A Cauchy elastic material is also called a simple elastic material.
Unlike in a hyperelastic material
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
(which is sometimes referred to as Green elastic material), the work done by stresses does depend on the path of deformation. Therefore a Cauchy elastic material has a non-conservative structure and the stress cannot be derived from a scalar potential function.
A Cauchy elastic material must satisfy the requirements of material objectivity
Objectivity (frame invariance)
The concept of objectivity in science means that qualitative and quantitative descriptions of physical phenomena remain unchanged when the phenomena are observed under a variety of conditions...
and the principle of local action, i.e., the constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
s are spatially local. This assumption excludes action at a distance from being present in a constitutive relation (no nonlocal materials allowed). Also it enforces the requirement that body forces, such as gravity, and inertial forces cannot affect the properties of the material.
Though a Cauchy elastic material is a mathematical idealization of elastic material behavior, this description applies to many of the purely mechanical constitutive relations for elastic materials found in nature.
Constitutive equation
Neglecting the effect of temperature and assuming the body to be homogeneous, a constitutive equationConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
for the Cauchy stress tensor
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
can be formulated based on the deformation gradient:
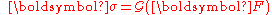
where
is the Cauchy stress and is the deformation gradient. Note that the function depends on the choice of reference configuration.Frame indifference
Objectivity (frame invariance)
The concept of objectivity in science means that qualitative and quantitative descriptions of physical phenomena remain unchanged when the phenomena are observed under a variety of conditions...
requires that the constitutive relation
should not change when the location of the observer changes. Therefore the constitutive equationConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
for another arbitrary observer can be written
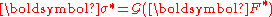. Knowing that the Cauchy stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and the deformation gradient are objective quantities, one can write: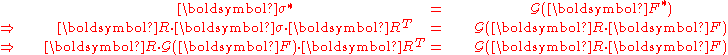where
is a proper orthogonal tensor.The above is a condition that the constitutive law
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
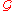has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive lawsConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
relating the deformation gradient to the first or second Piola-Kirchhoff stress tensor.
Isotropic Cauchy-elastic materials
For an isotropic material the Cauchy stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
can be expressed as a function of the left Cauchy-Green tensor 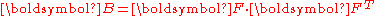. The constitutive equationConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
may then be written:
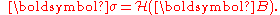
In order to find the restriction on
which will ensure the principle of material frame-indifference, one can write: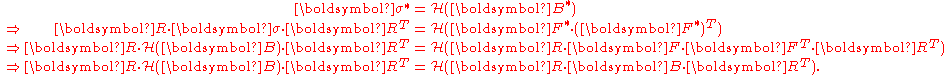A constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
that respects the above condition is said to be isotropic.