
Objectivity (frame invariance)
Encyclopedia
The concept of objectivity in science means that qualitative and quantitative descriptions of physical phenomena remain unchanged when the phenomena are observed under a variety of conditions. For example, physical processes (e.g. material properties) are invariant under changes of observers; that is, it is possible to reconcile observations of the process into a single coherent description of it.
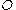 . In Euclidean three-dimensional space
. In Euclidean three-dimensional space
and time, an observer can measure relative positions of points in space and intervals of time.
Consider an event in Euclidean space
characterized by the pairs and
and 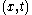 where
where  is a position vector and
is a position vector and  is a scalar representing time. This pair is mapped to another one denoted by the
is a scalar representing time. This pair is mapped to another one denoted by the  superscript. This mapping is done with the orthogonal time-dependent second order tensor
superscript. This mapping is done with the orthogonal time-dependent second order tensor 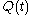 in a way such that the distance between the pairs is kept the same. Therefore one can write:
in a way such that the distance between the pairs is kept the same. Therefore one can write:

By introducing a vector
 and a real number
and a real number  denoting the time shift, the relationship between
denoting the time shift, the relationship between  and
and 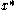 can be expressed
can be expressed
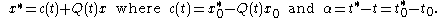
The one-to-one mapping connection of the pair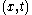 with its corresponding pair
with its corresponding pair 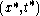 is referred to as a Euclidean transformation.
is referred to as a Euclidean transformation.
should be invariant relative to a change of observer. Consider one event recorded by two observers; for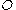 , point
, point  moves to position
moves to position 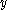 whereas for
whereas for 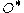 , the same point
, the same point 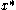 moves to
moves to 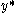 . For
. For 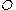 , the displacement is
, the displacement is 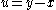 . On the other hand, for
. On the other hand, for  , one can write:
, one can write:
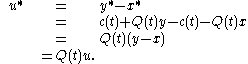
Any spatial vector field
 that transforms such that:
that transforms such that:
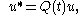
is said to be objective, since .
.
 is a rotation matrix,
is a rotation matrix, 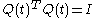 where
where 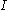 is the identity matrix
is the identity matrix
. Using this relation, the inverse of the Euclidean transformation can be written as:
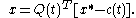
The velocity
can be obtained by differentiating the above expression:

By reorganizing the terms in the above equation, one can obtain:
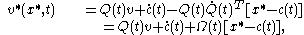
where
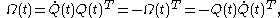
is a skew tensor
representing the spin of the reference frame of observer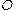 relative to the reference frame of observer
relative to the reference frame of observer 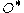 (Holzapfel 2000). To simplify the mathematical notation, the arguments of functions will no longer be written.
(Holzapfel 2000). To simplify the mathematical notation, the arguments of functions will no longer be written.
From the above expression, one can conclude that velocity
is not objective because of the presence of the extra terms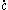 and
and 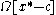 . Nevertheless, the velocity
. Nevertheless, the velocity
field can be made objective by constraining the change of observer to:
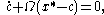
A time-independent rigid transformation such as:
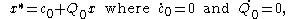
respects this condition.
 returns the spatial acceleration
returns the spatial acceleration
 . By differentiating the transformation law for the spatial velocity
. By differentiating the transformation law for the spatial velocity
, one can obtain:
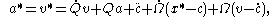
which can be rewritten as the following:
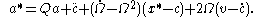
Just like the spatial velocity
, the acceleration
is not an objective quantity for a general change of observer (Holzapfel 2000). As for the spatial velocity
, the acceleration
can also be made objective by constraining the change of observer. One possibility would be to use the time-independent rigid transformation introduced above.
of order and denoted
and denoted 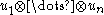 is objective if, during a general change of observer, the transformation is given by:
is objective if, during a general change of observer, the transformation is given by:
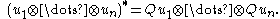
 , one can find with the above definition of objectivity that:
, one can find with the above definition of objectivity that:
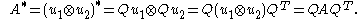
of order can be applied to a scalar field
can be applied to a scalar field
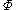 for which
for which 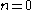 . The transformation would give:
. The transformation would give:
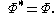
Physically, this means that a scalar field
is independent of the observer. Temperature is an example of scalar field
and it is easy to understand that the temperature at a given point in a room and at a given time would have the same value for any observer.
 and at its associated point
and at its associated point 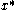 is a second order tensor
is a second order tensor
given by:
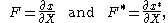
where represents the material coordinates. Using the chain rule
represents the material coordinates. Using the chain rule
, one can write:
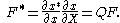
From the above equation, one can conclude that the deformation gradient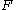 is objective even though it transforms like a vector
is objective even though it transforms like a vector
and not like a second order tensor
. This is because one index of the tensor
describes the material coordinates which are independent of the observer (Holzapfel 2000).
which are independent of the observer (Holzapfel 2000).
 is related to the Cauchy stress tensor
is related to the Cauchy stress tensor
 at a given point
at a given point  by the outward normal to the surface
by the outward normal to the surface  such that:
such that: 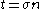 . The Cauchy traction vector
. The Cauchy traction vector
for another observer can be simply written as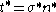 , where
, where  and
and  are both objective vectors. Knowing that, one can write:
are both objective vectors. Knowing that, one can write:
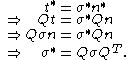
This demonstrates that the Cauchy stress tensor
is objective.
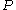 is defined as:
is defined as:

where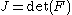 . It is also interesting to know that since
. It is also interesting to know that since 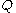 is a rotation matrix:
is a rotation matrix:
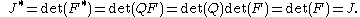
Using identities developed previously, one can write:
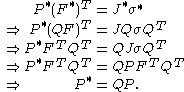
This proves that the first Piola-Kirchhoff stress tensor is objective. Similarly to the deformation gradient, this second order tensor
transforms like a vector
.
The second Piola-Kirchhoff stress tensor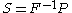 is also objective and transforms like a scalar field
is also objective and transforms like a scalar field
. This can be easily demonstrated:
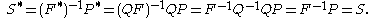
The three stress tensors, ,
, 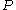 and
and  , studied here were all found to be objective. Therefore, they are all suitable to describe the material response and develop constitutive laws, since they are independent of the observer.
, studied here were all found to be objective. Therefore, they are all suitable to describe the material response and develop constitutive laws, since they are independent of the observer.
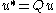 and an objective tensor
and an objective tensor 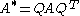 usually do not conserve their objectivity through time differentiation as demonstrated below:
usually do not conserve their objectivity through time differentiation as demonstrated below:
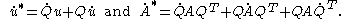
Objectivity rates are modified material derivatives that allows to have an objective time differentiation. Before presenting some examples of objectivity rates, certain other quantities need to be introduced. First, the spatial velocity gradient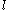 is defined as:
is defined as:
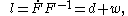
where is a symmetric tensor and
is a symmetric tensor and 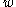 is a skew tensor
is a skew tensor
called the spin tensor. For a given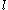 ,
, 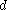 and
and 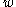 are uniquely defined. The Euclidean transformation for the spatial velocity gradient can be written as:
are uniquely defined. The Euclidean transformation for the spatial velocity gradient can be written as:
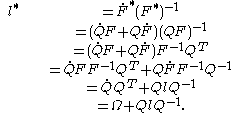
Substituting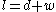 in the above equation, one can obtain two following relations:
in the above equation, one can obtain two following relations:
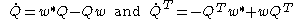
Substituting the above result in the previously obtained equation for the rate of an objective vector, one can write:
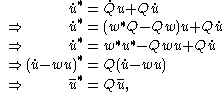
where the co-rotational rate of the objective vector field is defined as:
is defined as: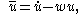
and represents an objective quantity. Similarly, using the above equations, one can obtain the co-rotational rate of the objective second-order tensor field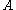 :
:
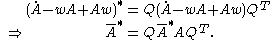
This co-rotational rate second order tensor is defined as:
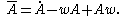
This objective rate is known as the Jaumann-Zaremba rate and it is often used in plasticity theory. Many different objective rates can be developed and the reader should refer to Holzapfel 2000 for more details.
.
Neglecting the effect of temperature and assuming the body to be homogeneous, a constitutive equation
for the Cauchy stress tensor
can be formulated based on the deformation gradient:
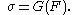
This constitutive equation
for another arbitrary observer can be written . Knowing that the Cauchy stress tensor
. Knowing that the Cauchy stress tensor
 and the deformation gradient
and the deformation gradient 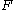 are objective quantities, one can write:
are objective quantities, one can write:
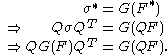
The above is a condition that the constitutive law
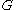 has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive laws
has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive laws
relating the deformation gradient to the first or second Piola-Kirchhoff stress tensor.
 is a function of the left Cauchy-Green tensor
is a function of the left Cauchy-Green tensor 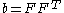 . The constitutive equation
. The constitutive equation
may be written:
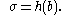
In order to find the restriction on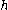 which will ensure the principle of material frame-indifference, one can write:
which will ensure the principle of material frame-indifference, one can write:
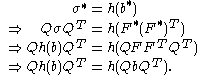
A constitutive equation
that respects the above condition is said to be isotropic (Holzapfel 2000). Physically, this characteristic means that the material has no preferential direction. Wood and most fibre-reinforced composites are generally stronger in the direction of their fibres therefore they are not isotropic materials (they are qualified as anisotropic).
Euclidean transformation
Physical processes can be described by an observer denoted by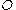 . In Euclidean three-dimensional space
. In Euclidean three-dimensional spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and time, an observer can measure relative positions of points in space and intervals of time.
Consider an event in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
characterized by the pairs
 and
and 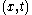 where
where  is a position vector and
is a position vector and  is a scalar representing time. This pair is mapped to another one denoted by the
is a scalar representing time. This pair is mapped to another one denoted by the  superscript. This mapping is done with the orthogonal time-dependent second order tensor
superscript. This mapping is done with the orthogonal time-dependent second order tensor 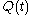 in a way such that the distance between the pairs is kept the same. Therefore one can write:
in a way such that the distance between the pairs is kept the same. Therefore one can write:
By introducing a vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
 and a real number
and a real number  denoting the time shift, the relationship between
denoting the time shift, the relationship between  and
and 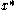 can be expressed
can be expressed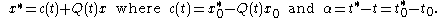
The one-to-one mapping connection of the pair
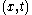 with its corresponding pair
with its corresponding pair 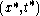 is referred to as a Euclidean transformation.
is referred to as a Euclidean transformation.Displacement
A physical quantity like displacementDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
should be invariant relative to a change of observer. Consider one event recorded by two observers; for
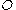 , point
, point  moves to position
moves to position 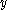 whereas for
whereas for 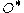 , the same point
, the same point 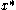 moves to
moves to 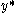 . For
. For 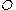 , the displacement is
, the displacement is 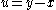 . On the other hand, for
. On the other hand, for  , one can write:
, one can write: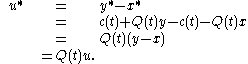
Any spatial vector field
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
 that transforms such that:
that transforms such that: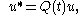
is said to be objective, since
 .
.Velocity
Because is a rotation matrix,
is a rotation matrix, 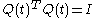 where
where 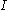 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Using this relation, the inverse of the Euclidean transformation can be written as:
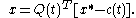
The velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
can be obtained by differentiating the above expression:

By reorganizing the terms in the above equation, one can obtain:
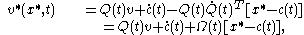
where
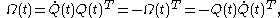
is a skew tensor
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
representing the spin of the reference frame of observer
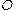 relative to the reference frame of observer
relative to the reference frame of observer 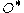 (Holzapfel 2000). To simplify the mathematical notation, the arguments of functions will no longer be written.
(Holzapfel 2000). To simplify the mathematical notation, the arguments of functions will no longer be written.From the above expression, one can conclude that velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
is not objective because of the presence of the extra terms
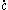 and
and 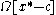 . Nevertheless, the velocity
. Nevertheless, the velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
field can be made objective by constraining the change of observer to:
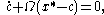
A time-independent rigid transformation such as:
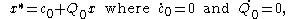
respects this condition.
Acceleration
The material time derivative of the spatial velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
 returns the spatial acceleration
returns the spatial accelerationAcceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
 . By differentiating the transformation law for the spatial velocity
. By differentiating the transformation law for the spatial velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, one can obtain:
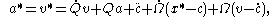
which can be rewritten as the following:
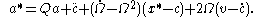
Just like the spatial velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
is not an objective quantity for a general change of observer (Holzapfel 2000). As for the spatial velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
can also be made objective by constraining the change of observer. One possibility would be to use the time-independent rigid transformation introduced above.
Objectivity for higher-order tensor fields
A tensor fieldTensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
of order
 and denoted
and denoted 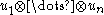 is objective if, during a general change of observer, the transformation is given by:
is objective if, during a general change of observer, the transformation is given by: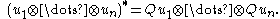
Example for a second order tensor
Introducing a second order tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
 , one can find with the above definition of objectivity that:
, one can find with the above definition of objectivity that: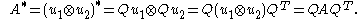
Example for a scalar field
The general condition of objectivity for a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of order
 can be applied to a scalar field
can be applied to a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
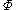 for which
for which 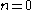 . The transformation would give:
. The transformation would give: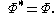
Physically, this means that a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
is independent of the observer. Temperature is an example of scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
and it is easy to understand that the temperature at a given point in a room and at a given time would have the same value for any observer.
Deformation gradient
The deformation gradient at point and at its associated point
and at its associated point 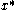 is a second order tensor
is a second order tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
given by:
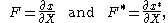
where
 represents the material coordinates. Using the chain rule
represents the material coordinates. Using the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, one can write:
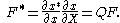
From the above equation, one can conclude that the deformation gradient
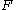 is objective even though it transforms like a vector
is objective even though it transforms like a vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
and not like a second order tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. This is because one index of the tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
describes the material coordinates
 which are independent of the observer (Holzapfel 2000).
which are independent of the observer (Holzapfel 2000).Cauchy stress tensor
The Cauchy traction vectorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
 is related to the Cauchy stress tensor
is related to the Cauchy stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
 at a given point
at a given point  by the outward normal to the surface
by the outward normal to the surface  such that:
such that: 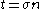 . The Cauchy traction vector
. The Cauchy traction vectorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
for another observer can be simply written as
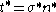 , where
, where  and
and  are both objective vectors. Knowing that, one can write:
are both objective vectors. Knowing that, one can write: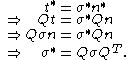
This demonstrates that the Cauchy stress tensor
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is objective.
Piola-Kirchhoff stress tensors
The first Piola-Kirchhoff stress tensor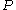 is defined as:
is defined as:
where
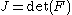 . It is also interesting to know that since
. It is also interesting to know that since 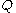 is a rotation matrix:
is a rotation matrix: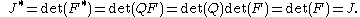
Using identities developed previously, one can write:
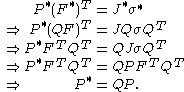
This proves that the first Piola-Kirchhoff stress tensor is objective. Similarly to the deformation gradient, this second order tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
transforms like a vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
.
The second Piola-Kirchhoff stress tensor
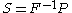 is also objective and transforms like a scalar field
is also objective and transforms like a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. This can be easily demonstrated:
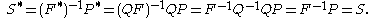
The three stress tensors,
 ,
, 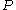 and
and  , studied here were all found to be objective. Therefore, they are all suitable to describe the material response and develop constitutive laws, since they are independent of the observer.
, studied here were all found to be objective. Therefore, they are all suitable to describe the material response and develop constitutive laws, since they are independent of the observer.Objectivity rates
It was shown above that even if a displacement field is objective, the velocity field is not. An objective vector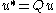 and an objective tensor
and an objective tensor 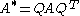 usually do not conserve their objectivity through time differentiation as demonstrated below:
usually do not conserve their objectivity through time differentiation as demonstrated below: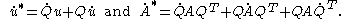
Objectivity rates are modified material derivatives that allows to have an objective time differentiation. Before presenting some examples of objectivity rates, certain other quantities need to be introduced. First, the spatial velocity gradient
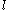 is defined as:
is defined as: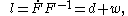
where
 is a symmetric tensor and
is a symmetric tensor and 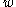 is a skew tensor
is a skew tensorSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
called the spin tensor. For a given
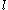 ,
, 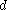 and
and 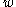 are uniquely defined. The Euclidean transformation for the spatial velocity gradient can be written as:
are uniquely defined. The Euclidean transformation for the spatial velocity gradient can be written as: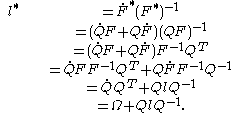
Substituting
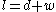 in the above equation, one can obtain two following relations:
in the above equation, one can obtain two following relations: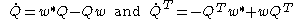
Substituting the above result in the previously obtained equation for the rate of an objective vector, one can write:
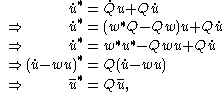
where the co-rotational rate of the objective vector field
 is defined as:
is defined as: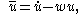
and represents an objective quantity. Similarly, using the above equations, one can obtain the co-rotational rate of the objective second-order tensor field
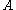 :
: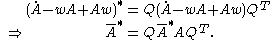
This co-rotational rate second order tensor is defined as:
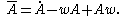
This objective rate is known as the Jaumann-Zaremba rate and it is often used in plasticity theory. Many different objective rates can be developed and the reader should refer to Holzapfel 2000 for more details.
Invariance of material response
The principal of material invariance basically means that the material properties are independent of the observer. In this section it will be shown how this principle adds constraints to constitutive lawsConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
.
Cauchy-elastic materials
A Cauchy-elastic material depends only on the current state of deformation at a given time (Holzapfel 2000). In other words, the material is independent of the deformation path and time.Neglecting the effect of temperature and assuming the body to be homogeneous, a constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
for the Cauchy stress tensor
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
can be formulated based on the deformation gradient:
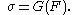
This constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
for another arbitrary observer can be written
 . Knowing that the Cauchy stress tensor
. Knowing that the Cauchy stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
 and the deformation gradient
and the deformation gradient 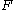 are objective quantities, one can write:
are objective quantities, one can write: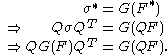
The above is a condition that the constitutive law
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
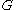 has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive laws
has to respect to make sure that the response of the material will be independent of the observer. Similar conditions can be derived for constitutive lawsConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
relating the deformation gradient to the first or second Piola-Kirchhoff stress tensor.
Isotropic Cauchy-elastic materials
Here, it will be assumed that the Cauchy stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
 is a function of the left Cauchy-Green tensor
is a function of the left Cauchy-Green tensor 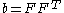 . The constitutive equation
. The constitutive equationConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
may be written:
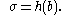
In order to find the restriction on
 which will ensure the principle of material frame-indifference, one can write:
which will ensure the principle of material frame-indifference, one can write: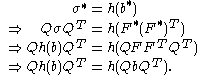
A constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
that respects the above condition is said to be isotropic (Holzapfel 2000). Physically, this characteristic means that the material has no preferential direction. Wood and most fibre-reinforced composites are generally stronger in the direction of their fibres therefore they are not isotropic materials (they are qualified as anisotropic).
See also
- Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
- Finite strain theory
- Lagrangian and Eulerian coordinatesLagrangian and Eulerian coordinatesIn fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...
- Piola-Kirchhoff stress tensor
- Stress (physics)Stress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...

