
String operations
Encyclopedia
In computer science
, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used on computer programming
, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms.

 be its alphabet. A string substitution or simply a substitution is a mapping f that maps letters in
be its alphabet. A string substitution or simply a substitution is a mapping f that maps letters in 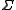 to languages (possibly in a different alphabet). Thus, for example, given a letter
to languages (possibly in a different alphabet). Thus, for example, given a letter 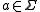 , one has
, one has 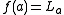 where
where 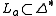 is some language whose alphabet is
is some language whose alphabet is  . This mapping may be extended to strings as
. This mapping may be extended to strings as
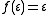
for the empty string
 , and
, and
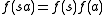
for string . String substitution may be extended to the entire language as
. String substitution may be extended to the entire language as
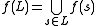
An example of string substitution occurs in regular language
s, which are closed under string substitution. That is, if the letters of a regular language are substituted by other regular languages, the result is still a regular language.
Another example is the conversion of an EBCDIC
-encoded string to ASCII
.
in formal language theory) is a string substitution such that each letter is replaced by a single string. That is, , where s is a string, for each letter a. String homomorphisms are homomorphism
, where s is a string, for each letter a. String homomorphisms are homomorphism
s, preserving the binary operation
of string concatenation. Given a language L, the set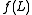 is called the homomorphic image of L. The inverse homomorphic image of a string s is defined as
is called the homomorphic image of L. The inverse homomorphic image of a string s is defined as
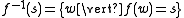
while the inverse homomorphic image of a language L is defined as
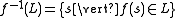
Note that, in general,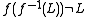 , while one does have
, while one does have
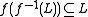
and
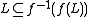
for any language L.
A string homomorphism is said to be -free (or e-free) if
-free (or e-free) if 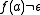 for all
for all  in
in  . Simple single-letter substitution cipher
. Simple single-letter substitution cipher
s are examples of ( -free) string homomorphisms.
-free) string homomorphisms.
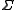 is an alphabet, the string projection of s is the string that results by removing all letters which are not in
is an alphabet, the string projection of s is the string that results by removing all letters which are not in 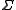 . It is written as
. It is written as 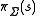 . It is formally defined by removal of letters from the right hand side:
. It is formally defined by removal of letters from the right hand side:

Here denotes the empty string
denotes the empty string
. The projection of a string is essentially the same as a projection in relational algebra.
String projection may be promoted to the projection of a language. Given a formal language
L, its projection is given by

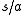 . If the string does not have a on the right hand side, the result is the empty string. Thus:
. If the string does not have a on the right hand side, the result is the empty string. Thus:

The quotient of the empty string may be taken:

Similarly, given a subset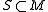 of a monoid
of a monoid 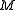 , one may define the quotient subset as
, one may define the quotient subset as

Left quotients may be defined similarly, with operations taking place on the left of a string.
 of a monoid
of a monoid  defines an equivalence relation
defines an equivalence relation
, called the right syntactic relation of S. It is given by
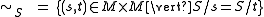
The relation is clearly of finite index (has a finite number of equivalence classes) if and only if the family right quotients is finite; that is, if
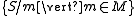
is finite. In this case, S is a recognizable language
, that is, a language that can be recognized by a finite state automaton. This is discussed in greater detail in the article on syntactic monoid
s.
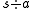 and is recursively defined as
and is recursively defined as
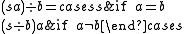
The empty string is always cancellable:

Clearly, right cancellation and projection commute
:

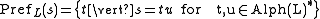
here .
.
The prefix closure of a language is
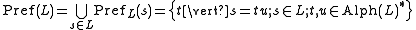
Example:
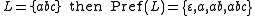
A language is called prefix closed if .
.
The prefix closure operator is idempotent:

The prefix relation is a binary relation
 such that
such that  if and only if
if and only if  .
.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used on computer programming
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms.
Alphabet of a string
The alphabet of a string is a list of all of the letters that occur in a particular string. If s is a string, its alphabet is denoted by
String substitution
Let L be a language, and let be its alphabet. A string substitution or simply a substitution is a mapping f that maps letters in
be its alphabet. A string substitution or simply a substitution is a mapping f that maps letters in 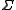 to languages (possibly in a different alphabet). Thus, for example, given a letter
to languages (possibly in a different alphabet). Thus, for example, given a letter 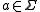 , one has
, one has 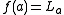 where
where 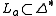 is some language whose alphabet is
is some language whose alphabet is  . This mapping may be extended to strings as
. This mapping may be extended to strings as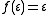
for the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
 , and
, and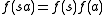
for string
 . String substitution may be extended to the entire language as
. String substitution may be extended to the entire language as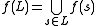
An example of string substitution occurs in regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s, which are closed under string substitution. That is, if the letters of a regular language are substituted by other regular languages, the result is still a regular language.
Another example is the conversion of an EBCDIC
EBCDIC
Extended Binary Coded Decimal Interchange Code is an 8-bit character encoding used mainly on IBM mainframe and IBM midrange computer operating systems....
-encoded string to ASCII
ASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
.
String homomorphism
A string homomorphism (often referred to simply as a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
in formal language theory) is a string substitution such that each letter is replaced by a single string. That is,
 , where s is a string, for each letter a. String homomorphisms are homomorphism
, where s is a string, for each letter a. String homomorphisms are homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s, preserving the binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
of string concatenation. Given a language L, the set
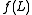 is called the homomorphic image of L. The inverse homomorphic image of a string s is defined as
is called the homomorphic image of L. The inverse homomorphic image of a string s is defined as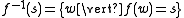
while the inverse homomorphic image of a language L is defined as
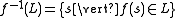
Note that, in general,
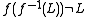 , while one does have
, while one does have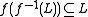
and
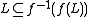
for any language L.
A string homomorphism is said to be
 -free (or e-free) if
-free (or e-free) if 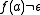 for all
for all  in
in  . Simple single-letter substitution cipher
. Simple single-letter substitution cipherSubstitution cipher
In cryptography, a substitution cipher is a method of encryption by which units of plaintext are replaced with ciphertext according to a regular system; the "units" may be single letters , pairs of letters, triplets of letters, mixtures of the above, and so forth...
s are examples of (
 -free) string homomorphisms.
-free) string homomorphisms.String projection
If s is a string, and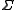 is an alphabet, the string projection of s is the string that results by removing all letters which are not in
is an alphabet, the string projection of s is the string that results by removing all letters which are not in 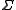 . It is written as
. It is written as 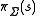 . It is formally defined by removal of letters from the right hand side:
. It is formally defined by removal of letters from the right hand side:
Here
 denotes the empty string
denotes the empty stringEmpty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
. The projection of a string is essentially the same as a projection in relational algebra.
String projection may be promoted to the projection of a language. Given a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
L, its projection is given by

Right quotient
The right quotient of a letter a from a string s is the truncation of the letter a in the string s, from the right hand side. It is denoted as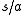 . If the string does not have a on the right hand side, the result is the empty string. Thus:
. If the string does not have a on the right hand side, the result is the empty string. Thus:
The quotient of the empty string may be taken:

Similarly, given a subset
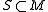 of a monoid
of a monoid 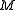 , one may define the quotient subset as
, one may define the quotient subset as
Left quotients may be defined similarly, with operations taking place on the left of a string.
Syntactic relation
The right quotient of a subset of a monoid
of a monoid  defines an equivalence relation
defines an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, called the right syntactic relation of S. It is given by
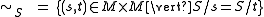
The relation is clearly of finite index (has a finite number of equivalence classes) if and only if the family right quotients is finite; that is, if
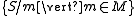
is finite. In this case, S is a recognizable language
Recognizable language
In mathematics and computer science, a recognizable language is a formal language that is recognized by a finite state machine. Equivalently, a recognizable language is one for which the family of quotients for the syntactic relation is finite.-Definition:...
, that is, a language that can be recognized by a finite state automaton. This is discussed in greater detail in the article on syntactic monoid
Syntactic monoid
In mathematics and computer science, the syntactic monoid M of a formal language L is the smallest monoid that recognizes the language L.-Syntactic quotient:...
s.
Right cancellation
The right cancellation of a letter a from a string s is the removal of the first occurrence of the letter a in the string s, starting from the right hand side. It is denoted as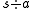 and is recursively defined as
and is recursively defined as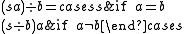
The empty string is always cancellable:

Clearly, right cancellation and projection commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
:

Prefixes
The prefixes of a string is the set of all prefixes to a string, with respect to a given language: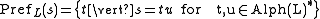
here
 .
.The prefix closure of a language is
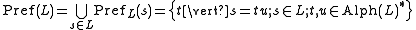
Example:
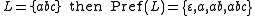
A language is called prefix closed if
 .
.The prefix closure operator is idempotent:

The prefix relation is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
 such that
such that  if and only if
if and only if  .
.

