
Structure of liquids and glasses
Encyclopedia
The structure of liquid
s and glass
es is characterized by the absence of long-range order
. It does, however, possess some short-range order as a result of nearest neighbour chemical bond
ing characteristics.
s in X-ray and neutron diffraction
. Under normal conditions, the diffraction pattern has circular symmetry, expressing the isotropy
of the liquid. In radial direction, the diffraction intensity exhibits smooth oscillations. This intensity is usually described by the static structure factor S(q), with scattering vector q=(4π/λ)sin(2θ), where λ denotes the wavelength of the probe (photon or neutron) and 2θ is the scattering angle (with a magnitude twice that of the Bragg angle θ). The high-q oscillations of S(q) express the local range order of the liquid, i.e. the correlations between a specific atom and it's the first shell of nearest neighbours.
A more intuitive description of these correlations is given by the radial distribution function
g(r), which is the Fourier transform
of S(q). It represents a spatial average of a temporal snapshot of pair correlations in the liquid.
g(r) is determined by a relatively simple calculation of the average number of particles found within a given volume of shell located at a distance r from the center. The average density of atoms at a given radial distance from the center is given by the formula:
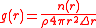
where n(r) is the mean number of atoms in a shell of width Δr at distance r, and ρ is the mean atom density.
g(r) provides a means of comparison between diffraction experiment and computer simulation. It can also be used in conjunction with the interatomic pair potential function in order to calculate such macroscopic thermodynamic parameters as the internal energy, Gibbs free energy, entropy and enthalpy of the disordered system.
A typical plot of g versus r shows a number of important features:
(NMR), X-ray absorption fine structure
(XAFS) and other spectroscopy methods including Raman spectroscopy
. Experimental measurements can be combined with computer simulation methods, such as Reverse Monte Carlo
(RMC) or molecular dynamics
(MD) simulations, to obtain more complete and detailed description of the atomic structure.
 Early theories relating to the structure of glass included the crystallite theory whereby glass is an aggregate of crystallite
Early theories relating to the structure of glass included the crystallite theory whereby glass is an aggregate of crystallite
s (extremely small crystals). However, structural determinations of vitreous SiO2 and GeO2 made by Warren and co-workers in the 1930s using x-ray diffraction showed the structure of glass to be typical of an amorphous solid
In 1932 Zachariasen introduced the random network theory of glass in which the nature of bonding in the glass is the same as in the crystal but where the basic structural units in a glass are connected in a random manner in contrast to the periodic arrangement in a crystalline material.
Despite the lack of long range order, the structure of glass does exhibit a high degree of ordering on short length scales due to the chemical bonding constraints in local atomic polyhedra. For example, the SiO4 tetrahedra that form the fundamental structural units in silica glass represent a high degree of order, i.e. every silicon atom is coordinated by 4 oxygen atoms and the nearest neighbour Si-O bond length exhibits only a narrow distribution throughout the structure. The tetrahedra in silica also form a network of ring structures which leads to ordering on more intermediate length scales of up to approximately 10 Angstrom
s.
As in other amorphous solid
s, the atomic structure of a glass lacks any long range translational periodicity
. However, due to chemical bonding characteristics glasses do possess a high degree of short-range order with respect to local atomic polyhedra.
It is deemed that the bonding structure of glasses, although disordered, has the same symmetry signature (Hausdorff-Besicovitch dimensionality
) as for crystalline materials.

line forms: quartz, tridymite, cistobalite, and others (including the high pressure polymorphs
Stishovite
and Coesite
). Nearly all of them involve tetrahedral SiO4 units linked together by shared vertices in different arrangements. Si-O bond lengths vary between the different crystal forms. For example, in α-quartz the bond length is 161 pm, whereas in α-tridymite it ranges from 154–171 pm. The Si-O-Si bond angle also varies from 140° in α-tridymite to 144° in α-quartz to 180° in β-tridymite.
), the SiO4 tetrahedra form a network that does not exhibit any long-range order. However, the tetrahedra themselves represent a high degree of local ordering, i.e. every silicon atom is coordinated by 4 oxygen atoms and the nearest neighbour Si-O bond length exhibits only a narrow distribution throughout the structure. Despite the lack of ordering on extended length scales, the tetrahedra also form a network of ring-like structures which lead to ordering on intermediate length scales (up to approximately 10 Angstroms or so). Under the application of high pressure (approximately 40 GPa) silica glass undergoes a continuous polyamorphic
phase transition into an octahedral form, i.e. the Si atoms are surrounded by 6 oxygen atoms instead of four in the ambient pressure tetrahedral glass.
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s and glass
Glass
Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
es is characterized by the absence of long-range order
Order and disorder (physics)
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system.In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered...
. It does, however, possess some short-range order as a result of nearest neighbour chemical bond
Chemical bond
A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
ing characteristics.
Diffraction, structure factor, pair correlations
The absence of long-range order in liquids and glasses is evidenced by the absence of Bragg peakBragg Peak
The Bragg peak is a pronounced peak on the Bragg curve which plots the energy loss of ionizing radiation during its travel through matter. For protons, α-rays, and other ion rays, the peak occurs immediately before the particles come to rest...
s in X-ray and neutron diffraction
Neutron diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of...
. Under normal conditions, the diffraction pattern has circular symmetry, expressing the isotropy
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
of the liquid. In radial direction, the diffraction intensity exhibits smooth oscillations. This intensity is usually described by the static structure factor S(q), with scattering vector q=(4π/λ)sin(2θ), where λ denotes the wavelength of the probe (photon or neutron) and 2θ is the scattering angle (with a magnitude twice that of the Bragg angle θ). The high-q oscillations of S(q) express the local range order of the liquid, i.e. the correlations between a specific atom and it's the first shell of nearest neighbours.
A more intuitive description of these correlations is given by the radial distribution function
Radial distribution function
In statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....
g(r), which is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of S(q). It represents a spatial average of a temporal snapshot of pair correlations in the liquid.
g(r) is determined by a relatively simple calculation of the average number of particles found within a given volume of shell located at a distance r from the center. The average density of atoms at a given radial distance from the center is given by the formula:
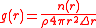
where n(r) is the mean number of atoms in a shell of width Δr at distance r, and ρ is the mean atom density.
g(r) provides a means of comparison between diffraction experiment and computer simulation. It can also be used in conjunction with the interatomic pair potential function in order to calculate such macroscopic thermodynamic parameters as the internal energy, Gibbs free energy, entropy and enthalpy of the disordered system.
A typical plot of g versus r shows a number of important features:
- At short separations (small r), g(r) = 0. This indicates the effective width of the atoms, which ultimately limits their distance of approach.
- A number of obvious peaks appear, at increasingly reduced intensities. The peaks indicate that the atoms pack around each other in 'shells' of nearest neighbors. At very long range, g(r) approaches a limiting value of 1 (or unity), which describes the average density at this range.
- The attenuation of the peaks at increasing radial distances from the center indicates the decreasing degree of order from the center particle. This illustrates vividly the origin of the term "short-range order" in classical liquids and glasses.
Other experimental techniques
Other experimental techniques often employed to study the structure of glasses include Nuclear Magnetic ResonanceNuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(NMR), X-ray absorption fine structure
X-ray absorption fine structure
X-ray absorption fine structure is a specific structure observed in X-ray absorption spectroscopy . By analyzing the XAFS, information can be acquired on the local structure and on the unoccupied electronic states.-Spectra:...
(XAFS) and other spectroscopy methods including Raman spectroscopy
Raman spectroscopy
Raman spectroscopy is a spectroscopic technique used to study vibrational, rotational, and other low-frequency modes in a system.It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range...
. Experimental measurements can be combined with computer simulation methods, such as Reverse Monte Carlo
Reverse Monte Carlo
-Introduction:The Reverse Monte Carlo modelling method is a variation of the standard Metropolis-Hastings algorithm to solve an inverse problem whereby a model is adjusted until its parameters have the greatest consistency with experimental data...
(RMC) or molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
(MD) simulations, to obtain more complete and detailed description of the atomic structure.
Network glasses

Crystallite
Crystallites are small, often microscopic crystals that, held together through highly defective boundaries, constitute a polycrystalline solid. Metallurgists often refer to crystallites as grains.- Details :...
s (extremely small crystals). However, structural determinations of vitreous SiO2 and GeO2 made by Warren and co-workers in the 1930s using x-ray diffraction showed the structure of glass to be typical of an amorphous solid
Amorphous solid
In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal....
In 1932 Zachariasen introduced the random network theory of glass in which the nature of bonding in the glass is the same as in the crystal but where the basic structural units in a glass are connected in a random manner in contrast to the periodic arrangement in a crystalline material.
Despite the lack of long range order, the structure of glass does exhibit a high degree of ordering on short length scales due to the chemical bonding constraints in local atomic polyhedra. For example, the SiO4 tetrahedra that form the fundamental structural units in silica glass represent a high degree of order, i.e. every silicon atom is coordinated by 4 oxygen atoms and the nearest neighbour Si-O bond length exhibits only a narrow distribution throughout the structure. The tetrahedra in silica also form a network of ring structures which leads to ordering on more intermediate length scales of up to approximately 10 Angstrom
Ångström
The angstrom or ångström, is a unit of length equal to 1/10,000,000,000 of a meter . Its symbol is the Swedish letter Å....
s.
As in other amorphous solid
Amorphous solid
In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal....
s, the atomic structure of a glass lacks any long range translational periodicity
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. However, due to chemical bonding characteristics glasses do possess a high degree of short-range order with respect to local atomic polyhedra.
It is deemed that the bonding structure of glasses, although disordered, has the same symmetry signature (Hausdorff-Besicovitch dimensionality
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
) as for crystalline materials.

Crystalline SiO2
Silica (the chemical compound SiO2) has a number of distinct crystalCrystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
line forms: quartz, tridymite, cistobalite, and others (including the high pressure polymorphs
Polymorphism (materials science)
Polymorphism in materials science is the ability of a solid material to exist in more than one form or crystal structure. Polymorphism can potentially be found in any crystalline material including polymers, minerals, and metals, and is related to allotropy, which refers to chemical elements...
Stishovite
Stishovite
Stishovite is an extremely hard, dense tetragonal form of silicon dioxide. It was long considered the hardest known oxide; however, boron suboxide has recently been discovered to be much harder...
and Coesite
Coesite
Coesite[p] is a form of silicon dioxide SiO2 that is formed when very high pressure , and moderately high temperature , are applied to quartz. Coesite was first synthesized by Loring Coes, Jr., a chemist at the Norton Company, in 1953. In 1960, coesite was found by Edward C. T...
). Nearly all of them involve tetrahedral SiO4 units linked together by shared vertices in different arrangements. Si-O bond lengths vary between the different crystal forms. For example, in α-quartz the bond length is 161 pm, whereas in α-tridymite it ranges from 154–171 pm. The Si-O-Si bond angle also varies from 140° in α-tridymite to 144° in α-quartz to 180° in β-tridymite.
Glassy SiO2
In amorphous silica (fused quartzFused quartz
Fused quartz and fused silica are types of glass containing primarily silica in amorphous form. They are manufactured using several different processes...
), the SiO4 tetrahedra form a network that does not exhibit any long-range order. However, the tetrahedra themselves represent a high degree of local ordering, i.e. every silicon atom is coordinated by 4 oxygen atoms and the nearest neighbour Si-O bond length exhibits only a narrow distribution throughout the structure. Despite the lack of ordering on extended length scales, the tetrahedra also form a network of ring-like structures which lead to ordering on intermediate length scales (up to approximately 10 Angstroms or so). Under the application of high pressure (approximately 40 GPa) silica glass undergoes a continuous polyamorphic
Polyamorphism
Polyamorphism is the ability of a substance to exist in several different amorphous modifications. It is analogous to the polymorphism of crystalline materials. Many amorphous substances can exist with different amorphous characteristics . However, polyamorphism requires two distinct amorphous...
phase transition into an octahedral form, i.e. the Si atoms are surrounded by 6 oxygen atoms instead of four in the ambient pressure tetrahedral glass.

