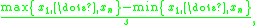Studentized range
Encyclopedia
In statistics
, the studentized range computed from a list x1, ..., xn of numbers is
where
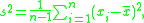
is the sample variance and

is the sample mean.
Generally, studentized
means adjusted by dividing by an estimate
of a population standard deviation
; see also studentized residual
. The concept is named after William Sealey Gosset, who wrote under the pseudonym "Student". The fact that the variance is a sample variance rather than the population variance, and thus something that differs from one random sample to the next, is essential to the definition, and complicates the problem of finding the probability distribution of any statistic that is studentized.
If X1, ..., Xn are independent identically distributed random variable
s that are normally distributed, the probability distribution of their studentized range is what is usually called the studentized range distribution. This probability distribution is the same regardless of the expected value
and standard deviation
of the normal distribution from which the sample is drawn: tables are available. This probability distribution has applications to hypothesis testing and multiple comparisons
. For example, the statistic can be used as a short-cut test, avoiding some calculations, in the analysis of variance
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the studentized range computed from a list x1, ..., xn of numbers is
where
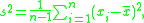
is the sample variance and

is the sample mean.
Generally, studentized
Studentization
In statistics, Studentization, named after William Sealy Gosset, who wrote under the pseudonym Student, is the adjustment consisting of division of a first-degree statistic derived from a sample, by a sample-based estimate of a population standard deviation...
means adjusted by dividing by an estimate
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
of a population standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
; see also studentized residual
Studentized residual
In statistics, a studentized residual is the quotient resulting from the division of a residual by an estimate of its standard deviation. Typically the standard deviations of residuals in a sample vary greatly from one data point to another even when the errors all have the same standard...
. The concept is named after William Sealey Gosset, who wrote under the pseudonym "Student". The fact that the variance is a sample variance rather than the population variance, and thus something that differs from one random sample to the next, is essential to the definition, and complicates the problem of finding the probability distribution of any statistic that is studentized.
If X1, ..., Xn are independent identically distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s that are normally distributed, the probability distribution of their studentized range is what is usually called the studentized range distribution. This probability distribution is the same regardless of the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of the normal distribution from which the sample is drawn: tables are available. This probability distribution has applications to hypothesis testing and multiple comparisons
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
. For example, the statistic can be used as a short-cut test, avoiding some calculations, in the analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
.
Further reading
- John Neter, Michael H. Kutner, Christopher J. Nachtsheim, William Wasserman (1996) Applied Linear Statistical Models, fourth edition, McGraw-Hill, page 726.
- John A. Rice (1995) Mathematical Statistics and Data Analysis, second edition, Duxbury Press, pages 451–452.