Subdivided interval categories
Encyclopedia
In mathematics
, more specifically category theory
, there exists an important collection of categories denoted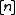
for natural numbers 
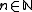. The objects of 
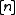are the integers 
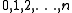, and the morphism set 
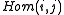for objects 
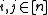is empty if 
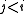and consists of a single element if 
.
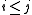Subdivided interval categories are very useful in defining simplicial sets
. The category whose objects are the subdivided interval categories and whose morphisms are functors is often written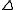
and is called the simplicial indexing category
. A simplicial set is just a contravariant functor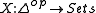
.
The category [1] has two objects and a single morphism between them. If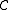
is any category, then 
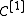is the category of morphisms and commutative squares in 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, there exists an important collection of categories denoted
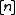for natural numbers 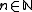. The objects of 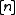are the integers 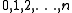, and the morphism set 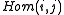for objects 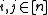is empty if 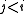and consists of a single element if 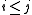.Subdivided interval categories are very useful in defining simplicial sets
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
. The category whose objects are the subdivided interval categories and whose morphisms are functors is often written
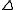and is called the simplicial indexing categorySimplicial category
In mathematics, the simplex category is the category of finite ordinals and order preserving maps. It is used to define simplicial and cosimplicial objects.-Formal definition:...
. A simplicial set is just a contravariant functor
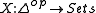.Examples
The category [0] is the one-object, one-morphism category. It is the terminal object in the category of small categories.The category [1] has two objects and a single morphism between them. If
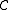is any category, then 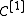is the category of morphisms and commutative squares in .