Subring test
Encyclopedia
In abstract algebra
, the subring test is a theorem
that states that for any ring
, a nonempty subset
of that ring is a subring
if it is closed under multiplication and subtraction. Note that here that the terms ring and subring are used without requiring a multiplicative identity element.
More formally, let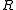
be a ring, and let 
be a nonempty subset of 
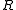. If for all 
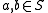one has 
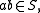and for all 
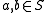one has 
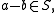then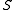 
is a subring of 
.
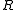If rings are required to have unity, then it must also be assumed that the multiplicative identity is in the subset.
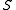is nonempty and closed under subtraction, by the subgroup test
it follows that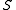
is a group
under addition. Hence,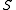
is closed under addition, addition is associative, 
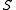has an additive identity, and every element in 
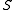has an additive inverse.
Since the operations of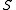
are the same as those of 
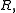it immediately follows that addition is commutative, multiplication is associative, multiplication is left distributive over addition, and multiplication is right distributive over addition.
Thus,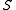
is a subring of 
.
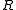Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the subring test is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
that states that for any ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, a nonempty subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of that ring is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
if it is closed under multiplication and subtraction. Note that here that the terms ring and subring are used without requiring a multiplicative identity element.
More formally, let
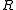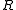be a ring, and let be a nonempty subset of . If for all 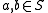one has 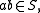and for all 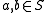one has 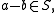then 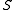is a subring of 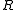.If rings are required to have unity, then it must also be assumed that the multiplicative identity is in the subset.
Proof
Since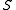 is nonempty and closed under subtraction, by the subgroup testSubgroup test
In Abstract Algebra, the one-step subgroup test is a theorem that states that for any group, a nonempty subset of that group is itself a group if the inverse of any element in the subset multiplied with any other element in the subset is also in the subset...
it follows that
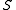is a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under addition. Hence,
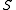is closed under addition, addition is associative, 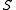has an additive identity, and every element in 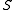has an additive inverse.Since the operations of
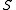are the same as those of 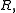it immediately follows that addition is commutative, multiplication is associative, multiplication is left distributive over addition, and multiplication is right distributive over addition.Thus,
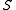is a subring of .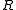