Succinct data structure
Encyclopedia
In computer science
, a succinct data structure is data structure
which uses an amount of space that is "close" to the information-theoretic lower bound, but (unlike other compressed representations) still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees
, and planar graph
s. Unlike general lossless data compression
algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure
, in which the size of the data structure depends upon the particular data being represented.
Suppose that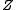
is the information-theoretical optimal number of bits needed to store some data. A representation of this data is called
Implicit structures are thus usually reduced to storing information using some permutation of the input data; the most well-known example of this is the heap.
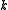-ary trees and multisets, as well as suffix tree
s and arrays
. The basic problem is to store a subset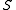
of a universe 
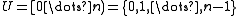, usually represented as a bit array 
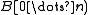where 
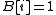iff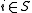 
. An indexable dictionary supports the usual methods on dictionaries (queries, and insertions/deletions in the dynamic case) as well as the following operations:
for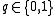
.
There is a simple representation which uses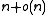
bits of storage space (the original bit array and an 
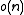auxiliary structure) and supports rank and select in constant time. It uses an idea similar to that for range-minimum queries
; there are a constant number of recursions before stopping at a subproblem of a limited size. The bit array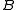
is partitioned into large blocks of size 
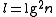bits and small blocks of size 
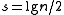bits. For each large block, the rank of its first bit is stored in a separate table 
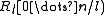; each such entry takes 
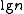bits for a total of 
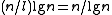bits of storage. Within a large block, another directory 
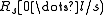stores the rank of each of the 
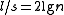small blocks it contains. The difference here is that it only needs 
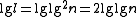bits for each entry, since only only the differences from the rank of the first bit in the containing large block need to be stored. Thus, this table takes a total of 
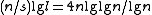bits. A lookup table 
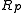can then be used that stores the answer to every possible rank query on a bit string of length 
for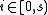 
; this requires 
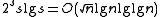bits of storage space. Thus, since each of these auxiliary tables take 
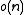space, this data structure supports rank queries in 
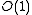time and 
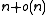bits of space.
To answer a query for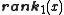
in constant time, a constant time algorithm computes
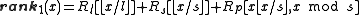
In practice, the lookup table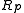
can be replaced by bitwise operations and smaller tables to perform find the number of bits set in the small blocks. This is often beneficial, since succinct data structures find their uses in large data sets, in which case cache misses become much more frequent and the chances of the lookup table being evicted from closer CPU caches becomes higher. Select queries can be easily supported by doing a binary search on the same auxiliary structure used for rank; however, this takes 
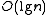time in the worst case. A more complicated structure using 
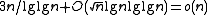bits of additional storage can be used to support select in constant time. In practice, many of these solutions have hidden constants in the 
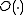notation which dominate before any asymptotic advantage becomes apparent; implementations using broadword operations and word-aligned blocks often perform better in practice.
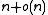space approach can be improved by noting that there are 
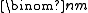distinct 
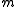-subsets of 
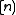(or binary strings of length 
with exactly 
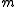1’s), and thus 
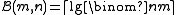is an information theoretic lower bound on the number of bits needed to store 
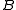. There is a succinct (static) dictionary which attains this bound, namely using 
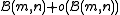space. This structure can be extended to support rank and select queries and takes 
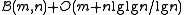space. This bound can be reduced to a space/time tradeoff by reducing the storage space of the dictionary to 
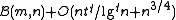with queries taking 
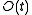time.
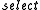function can quickly determine where each item begins, given its index.
Another example is the representation of a binary tree
: an arbitrary binary tree on n nodes can be represented in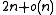
bits while supporting a variety of operations on any node, which includes finding its parent, its left and right child, and returning the size of its subtree, each in constant time. The number of different binary trees on 
nodes is 
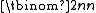
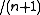. For large 
, this is about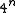 
; thus we need at least about 
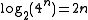bits to encode it. A succinct binary tree therefore would occupy only 
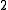bits per node.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a succinct data structure is data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
which uses an amount of space that is "close" to the information-theoretic lower bound, but (unlike other compressed representations) still allows for efficient query operations. The concept was originally introduced by Jacobson to encode bit vectors, (unlabeled) trees
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
, and planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s. Unlike general lossless data compression
Lossless data compression
Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. The term lossless is in contrast to lossy data compression, which only allows an approximation of the original data to be reconstructed, in exchange...
algorithms, succinct data structures retain the ability to use them in-place, without decompressing them first. A related notion is that of a compressed data structure
Compressed data structure
The term compressed data structure arises in the computer science subfields of algorithms, data structures, and theoretical computer science. It refers to a data structure whose operations are roughly as fast as those of a conventional data structure for the problem, but whose size can be...
, in which the size of the data structure depends upon the particular data being represented.
Suppose that
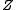is the information-theoretical optimal number of bits needed to store some data. A representation of this data is called- implicitImplicit data structureIn computer science, an implicit data structure is a data structure that uses very little memory besides the actual data elements i.e. very little information other than main data is stored in these structures. These are storage schemes which retain no pointers and represent the file of n k-key...
if it takes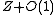
bits of space, - succinct if it takes
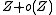bits of space, and - compact if it takes
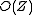bits of space.
Implicit structures are thus usually reduced to storing information using some permutation of the input data; the most well-known example of this is the heap.
Succinct dictionaries
Succinct indexable dictionaries, also called rank/select dictionaries, form the basis of a number of succinct representation techniques, including binary trees,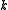-ary trees and multisets, as well as suffix treeSuffix tree
In computer science, a suffix tree is a data structure that presents the suffixes of a given string in a way that allows for a particularly fast implementation of many important string operations.The suffix tree for a string S is a tree whose edges are labeled with strings, such that each suffix...
s and arrays
Suffix array
In computer science, a suffix array is an array of integers giving the starting positions of suffixes of a string in lexicographical order.-Details:Consider the string...
. The basic problem is to store a subset
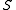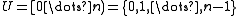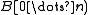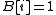of a universe , usually represented as a bit array where iff 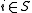. An indexable dictionary supports the usual methods on dictionaries (queries, and insertions/deletions in the dynamic case) as well as the following operations:
for
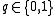.There is a simple representation which uses
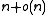bits of storage space (the original bit array and an 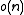auxiliary structure) and supports rank and select in constant time. It uses an idea similar to that for range-minimum queriesRange Minimum Query
Given an array A[1,n] of n ordered objects , a Range Minimum Query from i to j asks for the position of a minimum element in the sub-array A[i,j]....
; there are a constant number of recursions before stopping at a subproblem of a limited size. The bit array
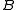is partitioned into large blocks of size 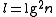bits and small blocks of size 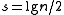bits. For each large block, the rank of its first bit is stored in a separate table 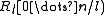; each such entry takes 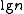bits for a total of 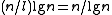bits of storage. Within a large block, another directory 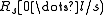stores the rank of each of the 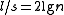small blocks it contains. The difference here is that it only needs 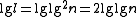bits for each entry, since only only the differences from the rank of the first bit in the containing large block need to be stored. Thus, this table takes a total of 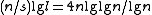bits. A lookup table 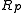can then be used that stores the answer to every possible rank query on a bit string of length for 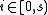; this requires 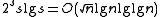bits of storage space. Thus, since each of these auxiliary tables take 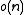space, this data structure supports rank queries in 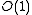time and 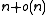bits of space.To answer a query for
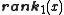in constant time, a constant time algorithm computes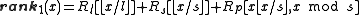In practice, the lookup table
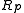can be replaced by bitwise operations and smaller tables to perform find the number of bits set in the small blocks. This is often beneficial, since succinct data structures find their uses in large data sets, in which case cache misses become much more frequent and the chances of the lookup table being evicted from closer CPU caches becomes higher. Select queries can be easily supported by doing a binary search on the same auxiliary structure used for rank; however, this takes 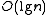time in the worst case. A more complicated structure using 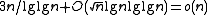bits of additional storage can be used to support select in constant time. In practice, many of these solutions have hidden constants in the 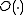notation which dominate before any asymptotic advantage becomes apparent; implementations using broadword operations and word-aligned blocks often perform better in practice.Entropy-compressed dictionaries
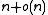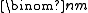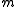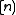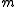The space approach can be improved by noting that there are distinct -subsets of (or binary strings of length with exactly 1’s), and thus 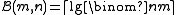is an information theoretic lower bound on the number of bits needed to store 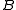. There is a succinct (static) dictionary which attains this bound, namely using 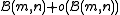space. This structure can be extended to support rank and select queries and takes 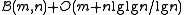space. This bound can be reduced to a space/time tradeoff by reducing the storage space of the dictionary to 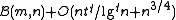with queries taking 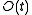time.Examples
When a sequence of variable-length items needs to be encoded, the items can simply be placed one after another, with no delimiters. A separate binary string consisting of 1s in the positions where an item begins, and 0s every where else is encoded along with it. Given this string, the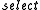 function can quickly determine where each item begins, given its index.Another example is the representation of a binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
: an arbitrary binary tree on n nodes can be represented in
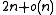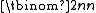
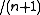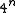bits while supporting a variety of operations on any node, which includes finding its parent, its left and right child, and returning the size of its subtree, each in constant time. The number of different binary trees on nodes is . For large , this is about ; thus we need at least about 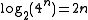bits to encode it. A succinct binary tree therefore would occupy only bits per node.