Sum of radicals
Encyclopedia
In computational complexity theory
there is an open problem whether some information about the sum of radicals may be computed in polynomial time depending on the input size, i.e., in the number of bits necessary to represent this sum. It is of importance for many problems in computational geometry
, since the computation of the Euclidean distance
between two points in general case involves the computation of a square root
, and therefore the perimeter
of a polygon
or the length of a polygonal chain takes the form of a sum of radicals.
The sum of radicals is defined as a finite linear combination
of radicals:
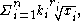
where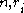
are natural number
s and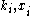
are real number
s.
Most theoretical research in computational geometry
of combinatorial character assumes the computational model
of infinite precision real RAM, i.e., an abstract computer in which real numbers and operations with them are performed with infinite precision and the input size of a real number and the cost of an elementary operation are constants. However there is research in computational complexity, especially in computer algebra, where the input size of a number is the number of bits necessary for its representation.
In particular, of interest in computational geometry is the problem of determining the sign
of the sum of radicals. For instance, the length of a polygonal path in which all vertices have integer coordinates may be expressed using the Pythagorean theorem
as a sum of integer square roots, so in order to determine whether one path is longer or shorter than another in a Euclidean shortest path
problem, it is necessary to determine the sign of an expression in which the first path's length is subtracted from the second; this expression is a sum of radicals.
In a similar way, the sum of radicals problem is inherent in the problem of minimum-weight triangulation in the Euclidean metric.
In 1991, Blömer proposed a polynomial time Monte Carlo algorithm
for determining whether a sum of radicals is zero, or more generally whether it represents a rational number.
While Blömer's result does not resolve the computational complexity of finding the sign of the sum of radicals, it does imply that if the latter problem is in class NP, then it is also in co-NP.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
there is an open problem whether some information about the sum of radicals may be computed in polynomial time depending on the input size, i.e., in the number of bits necessary to represent this sum. It is of importance for many problems in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, since the computation of the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between two points in general case involves the computation of a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, and therefore the perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
or the length of a polygonal chain takes the form of a sum of radicals.
The sum of radicals is defined as a finite linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of radicals:
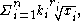
where
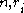are natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s and
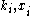are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
Most theoretical research in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
of combinatorial character assumes the computational model
Computational model
A computational model is a mathematical model in computational science that requires extensive computational resources to study the behavior of a complex system by computer simulation. The system under study is often a complex nonlinear system for which simple, intuitive analytical solutions are...
of infinite precision real RAM, i.e., an abstract computer in which real numbers and operations with them are performed with infinite precision and the input size of a real number and the cost of an elementary operation are constants. However there is research in computational complexity, especially in computer algebra, where the input size of a number is the number of bits necessary for its representation.
In particular, of interest in computational geometry is the problem of determining the sign
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
of the sum of radicals. For instance, the length of a polygonal path in which all vertices have integer coordinates may be expressed using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
as a sum of integer square roots, so in order to determine whether one path is longer or shorter than another in a Euclidean shortest path
Euclidean shortest path
The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles....
problem, it is necessary to determine the sign of an expression in which the first path's length is subtracted from the second; this expression is a sum of radicals.
In a similar way, the sum of radicals problem is inherent in the problem of minimum-weight triangulation in the Euclidean metric.
In 1991, Blömer proposed a polynomial time Monte Carlo algorithm
Monte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose running time is deterministic, but whose output may be incorrect with a certain probability....
for determining whether a sum of radicals is zero, or more generally whether it represents a rational number.
While Blömer's result does not resolve the computational complexity of finding the sign of the sum of radicals, it does imply that if the latter problem is in class NP, then it is also in co-NP.