
Super-prime
Encyclopedia
Super-prime numbers are the subsequence
of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers. The subsequence begins
That is, if p(i) denotes the ith prime number, the numbers in this sequence are those of the form p(p(i)). used a computer-aided proof (based on calculations involving the subset sum problem) to show that every integer greater than 96 may be represented as a sum of distinct super-prime numbers. Their proof relies on a result resembling Bertrand's postulate, stating that (after the larger gap between super-primes 5 and 11) each super-prime number is less than twice its predecessor in the sequence.
Broughan and Barnett show that there are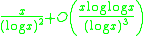
super-primes up to x.
One can also define "higher-order" primeness much the same way, and obtain analogous sequences of primes.
A variation on this theme is the sequence of prime numbers with palindromic
indices, beginning with
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers. The subsequence begins
- 3, 5, 11, 17, 31, 41, 59, 67, 83, 109, 127, 157, … .
That is, if p(i) denotes the ith prime number, the numbers in this sequence are those of the form p(p(i)). used a computer-aided proof (based on calculations involving the subset sum problem) to show that every integer greater than 96 may be represented as a sum of distinct super-prime numbers. Their proof relies on a result resembling Bertrand's postulate, stating that (after the larger gap between super-primes 5 and 11) each super-prime number is less than twice its predecessor in the sequence.
Broughan and Barnett show that there are
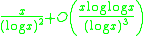
super-primes up to x.
One can also define "higher-order" primeness much the same way, and obtain analogous sequences of primes.
A variation on this theme is the sequence of prime numbers with palindromic
Palindromic number
A palindromic number or numeral palindrome is a 'symmetrical' number like 16461, that remains the same when its digits are reversed. The term palindromic is derived from palindrome, which refers to a word like rotor that remains unchanged under reversal of its letters...
indices, beginning with
- 3, 5, 11, 17, 31, 547, 739, 877, 1087, 1153, 2081, 2381, … .

