
Superconformal algebra
Encyclopedia
In theoretical physics
, the superconformal algebra is a graded Lie algebra
or superalgebra
that combines the conformal algebra and supersymmetry
. It generates the superconformal group in some cases (In two Euclidean dimensions, the Lie superalgebra
doesn't generate any Lie supergroup.).
In two dimensions, the superconformal algebra is infinite-dimensional. In higher dimensions, there is a finite number of known examples of superconformal algebras.
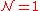 superconformal algebra in 3+1D is given by the bosonic generators
superconformal algebra in 3+1D is given by the bosonic generators  ,
,  ,
, 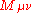 ,
,  , the U(1) R-symmetry
, the U(1) R-symmetry
 and the SU(N) R-symmetry
and the SU(N) R-symmetry 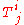 and the fermionic generators
and the fermionic generators  ,
, 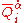 ,
,  and
and 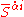 .
.  denote spacetime indices,
denote spacetime indices,  left-handed Weyl spinor indices and
left-handed Weyl spinor indices and  right-handed Weyl spinor indices, and
right-handed Weyl spinor indices, and  the internal R-symmetry indices.
the internal R-symmetry indices.
The Lie superbrackets are given by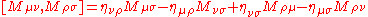
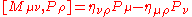
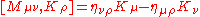
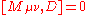


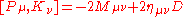
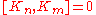
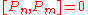
This is the bosonic conformal algebra
. Here, η is the Minkowski metric.
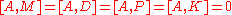
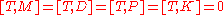
The bosonic conformal generators do not carry any R-charges.

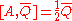
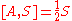


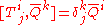
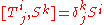
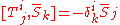
But the fermionic generators do.
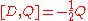



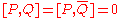
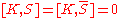
Tells us how the fermionic generators transform under bosonic conformal transformations.
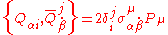

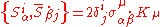
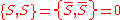
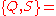

Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the superconformal algebra is a graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
or superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
that combines the conformal algebra and supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. It generates the superconformal group in some cases (In two Euclidean dimensions, the Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
doesn't generate any Lie supergroup.).
In two dimensions, the superconformal algebra is infinite-dimensional. In higher dimensions, there is a finite number of known examples of superconformal algebras.
Superconformal algebra in 3+1D
According to , the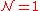 superconformal algebra in 3+1D is given by the bosonic generators
superconformal algebra in 3+1D is given by the bosonic generators  ,
,  ,
, 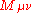 ,
,  , the U(1) R-symmetry
, the U(1) R-symmetryR-symmetry
In theoretical physics, the R-symmetry is the symmetry transforming different supercharges in a theory with supersymmetry into each other. In the simplest case of the N=1 supersymmetry, such an R-symmetry is isomorphic to a global U group or its discrete subgroup...
 and the SU(N) R-symmetry
and the SU(N) R-symmetry 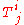 and the fermionic generators
and the fermionic generators  ,
, 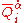 ,
,  and
and 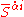 .
.  denote spacetime indices,
denote spacetime indices,  left-handed Weyl spinor indices and
left-handed Weyl spinor indices and  right-handed Weyl spinor indices, and
right-handed Weyl spinor indices, and  the internal R-symmetry indices.
the internal R-symmetry indices.The Lie superbrackets are given by
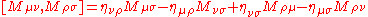
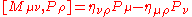
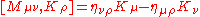
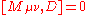


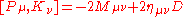
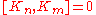
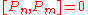
This is the bosonic conformal algebra
Conformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
. Here, η is the Minkowski metric.
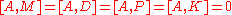
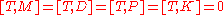
The bosonic conformal generators do not carry any R-charges.

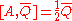
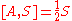


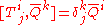
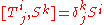
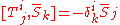
But the fermionic generators do.
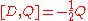



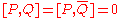
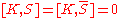
Tells us how the fermionic generators transform under bosonic conformal transformations.
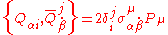

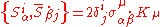
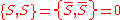
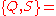

Superconformal algebra in 2D
See super Virasoro algebra. There are two possible algebras; a Neveu-Schwarz algebra and a Ramond algebra.See also
- Conformal symmetryConformal symmetryIn theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
- Super Virasoro algebra
- SUSY algebra

