
Superstrong cardinal
Encyclopedia
In mathematics
, a cardinal number
κ is called superstrong if and only if
there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point
κ and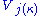 ⊆ M.
⊆ M.
Similarly, a cardinal κ is n-superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point
κ and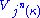 ⊆ M. Akihiro Kanamori
⊆ M. Akihiro Kanamori
has shown that the consistency strength of an n+1-superstrong cardinal exceeds that of an n-huge cardinal for each n > 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is called superstrong if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ and
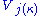 ⊆ M.
⊆ M.Similarly, a cardinal κ is n-superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ and
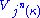 ⊆ M. Akihiro Kanamori
⊆ M. Akihiro KanamoriAkihiro Kanamori
is a Japan-born American mathematician. He specializes in set theory and is the author of the successful monograph on large cardinals, The Higher Infinite. He wrote several essays on the history of mathematics, especially set theory.Kanamori graduated from California Institute of Technology and...
has shown that the consistency strength of an n+1-superstrong cardinal exceeds that of an n-huge cardinal for each n > 0.

