
Supersymmetry as a quantum group
Encyclopedia
The concept in theoretical physics
of supersymmetry
can be reinterpreted in the language of noncommutative geometry
and quantum group
s. In particular, it involves a mild form of noncommutativity, namely supercommutativity.
. We have the two dimensional Hopf algebra
generated by (-1)F subject to
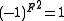
with the counit
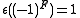
and the coproduct
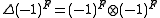
and the antipode
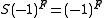
Thus far, there is nothing supersymmetric about this Hopf algebra at all; it is isomorphic to the Hopf algebra of the two element group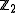 . Supersymmetry comes in when introducing the nontrivial quasitriangular structure
. Supersymmetry comes in when introducing the nontrivial quasitriangular structure
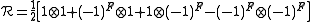
+1 eigenstates of (-1)^F are called bosons and -1 eigenstates fermions.
This describes a fermion
ic braiding; don't pick up a phase factor
when interchanging two bosons or a boson and a fermion, but multiply by -1 when interchanging two fermions. This gives us the essence of the boson/fermion distinction.
The Hopf algebra is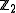 graded and contains even and odd elements. Even elements commute with (-1)F; odd ones anticommute. The subalgebra not containing (-1)^F is supercommutative.
graded and contains even and odd elements. Even elements commute with (-1)F; odd ones anticommute. The subalgebra not containing (-1)^F is supercommutative.
Let's say we are dealing with a super Lie algebra with even generators x and odd generators y.
Then,
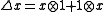

This is compatible with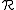 .
.
Supersymmetry is the symmetry over systems where interchanging two fermions picks up a minus sign.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
can be reinterpreted in the language of noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
and quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s. In particular, it involves a mild form of noncommutativity, namely supercommutativity.
(-1)F
Let's look at the essence of supersymmetry, which is encapsulated within the following minimal quantum groupQuantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
. We have the two dimensional Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
generated by (-1)F subject to
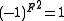
with the counit
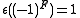
and the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
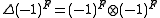
and the antipode
Antipode
Antipode, Antipodes, or Antipodeans may refer to:* Antipodal point, the diametrically opposite point on a sphere* Antipodes Water Company, a premium bottled water brand...
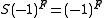
Thus far, there is nothing supersymmetric about this Hopf algebra at all; it is isomorphic to the Hopf algebra of the two element group
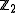 . Supersymmetry comes in when introducing the nontrivial quasitriangular structure
. Supersymmetry comes in when introducing the nontrivial quasitriangular structure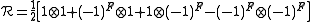
+1 eigenstates of (-1)^F are called bosons and -1 eigenstates fermions.
This describes a fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic braiding; don't pick up a phase factor
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
when interchanging two bosons or a boson and a fermion, but multiply by -1 when interchanging two fermions. This gives us the essence of the boson/fermion distinction.
fermionic operators
We still haven't introduced any actual supersymmetry yet, but we had set the stage by introducing the concept of fermions.The Hopf algebra is
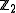 graded and contains even and odd elements. Even elements commute with (-1)F; odd ones anticommute. The subalgebra not containing (-1)^F is supercommutative.
graded and contains even and odd elements. Even elements commute with (-1)F; odd ones anticommute. The subalgebra not containing (-1)^F is supercommutative.Let's say we are dealing with a super Lie algebra with even generators x and odd generators y.
Then,
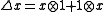

This is compatible with
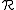 .
.Supersymmetry is the symmetry over systems where interchanging two fermions picks up a minus sign.

