Surface gradient
Encyclopedia
In vector calculus, the surface gradient is a vector differential operator
that is similar to the conventional gradient
. The distinction is that the surface gradient takes effect along a surface.
For a surface
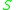in a scalar field
, the surface gradient is defined and notated as
where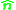
is a unit normal
to the surface. Examining the definition shows that the surface gradient is the (conventional) gradient with the component normal to the surface removed (subtracted), hence this gradient is tangent to the surface. In other words, the surface gradient is the orthographic projection
of the gradient onto the surface.
The surface gradient arises whenever the gradient of a quantity over a surface is important. In the study of capillary surface
s for example, the gradient of spatially varying surface tension
doesn't make much sense, however the surface gradient does and serves certain purposes.
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
that is similar to the conventional gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
. The distinction is that the surface gradient takes effect along a surface.
For a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
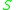in a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
, the surface gradient is defined and notated as where
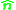is a unit normalSurface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the surface. Examining the definition shows that the surface gradient is the (conventional) gradient with the component normal to the surface removed (subtracted), hence this gradient is tangent to the surface. In other words, the surface gradient is the orthographic projection
Orthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
of the gradient onto the surface.
The surface gradient arises whenever the gradient of a quantity over a surface is important. In the study of capillary surface
Capillary surface
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces....
s for example, the gradient of spatially varying surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
doesn't make much sense, however the surface gradient does and serves certain purposes.