
Surface of general type
Encyclopedia
In algebraic geometry
, a surface of general type is an algebraic surface
with Kodaira dimension
2. Because of Chow's theorem any compact complex manifold of dimension 2 and with Kodaira dimension 2 will actually be an algebraic surface, and in some sense most surfaces are in this class.
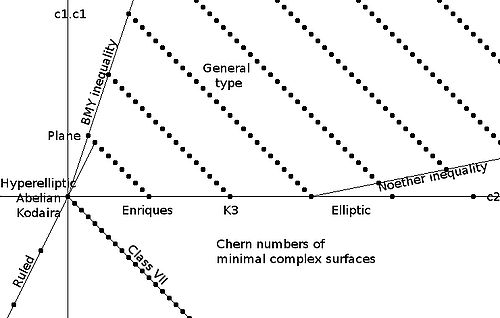 The study of which pairs of Chern numbers can occur for a surface of general type is known as "" and there is an almost complete answer to this question.
The study of which pairs of Chern numbers can occur for a surface of general type is known as "" and there is an almost complete answer to this question.
There are several conditions that the Chern numbers of a minimal
complex surface of general type must satisfy:
Many (and possibly all) pairs of integers satisfying these conditions are the Chern numbers for some complex surface of general type.
By contrast, for almost complex
surfaces, the only constraint is:
and this can always be realized.
These results follow from Reider's theorem
.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a surface of general type is an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
with Kodaira dimension
Kodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
2. Because of Chow's theorem any compact complex manifold of dimension 2 and with Kodaira dimension 2 will actually be an algebraic surface, and in some sense most surfaces are in this class.
Classification
Gieseker showed that there is a coarse moduli scheme for surfaces of general type; this means that for any fixed values of the Chern numbers c12 and c2, there is a quasi-projective scheme classifying the surfaces of general type with those Chern numbers. It remains a very difficult problem to describe these schemes explicitly, and there are few pairs of Chern numbers for which this has been done (except when the scheme is empty). There are some indications that these schemes are in general too complicated to write down explicitly: the known upper bounds for the number of components are very large, some components can be non-reduced everywhere, components may have many different dimensions, and the few pieces that have been studied explicitly tend to look rather complicated.
There are several conditions that the Chern numbers of a minimal
Minimal model
*In theoretical physics, the term minimal model usually refers to a special class of conformal field theories that generalize the Ising model, or to some closely related representations of the Virasoro algebra...
complex surface of general type must satisfy:
 (as it is equal to 12χ)
(as it is equal to 12χ)- c12 > 0, c2 > 0
- c12 ≤ 3c2 (the Bogomolov-Miyaoka-Yau inequality)
- 5c12 − c2 + 36 ≥ 12q ≥ 0 where q is the irregularity of a surfaceIrregularity of a surfaceIn mathematics, the irregularity of a complex surface X is the Hodge number h0,1= dim H1, usually denoted by q . The irregularity of an algebraic surface is sometimes defined to be this Hodge number, and sometimes defined to be the dimension of the Picard variety , which is the same in...
(the Noether inequalityNoether inequalityIn mathematics, the Noether inequality, named after Max Noether, is a property of compact minimal complex surfaces that restricts the topological type of the underlying topological 4-manifold...
).
Many (and possibly all) pairs of integers satisfying these conditions are the Chern numbers for some complex surface of general type.
By contrast, for almost complex
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
surfaces, the only constraint is:

and this can always be realized.
Examples
This is only a small selection of the rather large number of examples of surfaces of general type that have been found. Many of the surfaces of general type that have been investigated lie on (or near) the edges of the region of possible Chern numbers. In particular Horikawa surfaces lie on or near the "Noether line", many of the surfaces listed below lie on the line c2 + c12 = 12χ = 12, the minimum possible value for general type, and surfaces on the line 3c2 = c12 are all quotients of the unit ball in C2 (and are particularly hard to find).Surfaces with χ=1
These surface which are located in the "lower left" boundary in the diagram have been studied in detail. For these surfaces with second Chern class can be any integer from 3 to 11. Surfaces with all these values are known; a few of the many examples that have been studied are:- c2 = 3: Fake projective planeFake projective planeIn mathematics, a fake projective plane is one of the 50 complex algebraic surfaces that have the same Betti numbers as the projective plane, but are not isomorphic to it. Such objects are always algebraic surfaces of general type....
(Mumford surface). The first example was found by Mumford using p-adic geometry, and there are 50 examples altogether. They have the same Betti numbers as the projective plane, but are not homeomorphic to it as their fundamental groups are infinite. - c2 = 4: Beauville surfaceBeauville surfaceIn mathematics, a Beauville surface is one of the surfaces of general type introduced by . They are examples of "fake quadrics", with the same Betti numbers as quadric surfaces.-Construction:...
s are named for Arnaud Beauville and have infinite fundamental group. - c2 ≥ 4: Burniat surfaceBurniat surfaceIn mathematics, a Burniat surface is one of the surfaces of general type introduced by .-Invariants:The geometric genus and irregularity are both 0. The Chern number c12 is 2, 3, 4, 5, or 6....
s - c2 = 10: Campedelli surfaceCampedelli surfaceIn mathematics, a Campedelli surface is one of the surfaces of general type introduced by Campedelli.Surfaces with the same Hodge numbers are called numerical Campedelli surfaces.-Invariants:Hodge diamond:10 0080001...
s . Surfaces with the same Hodge numbers are called numerical Campedelli surfaces. - c2 = 10: Catanese surfaceCatanese surfaceIn mathematics, a Catanese surface is one of the surfaces of general type introduced by .-Construction:The construction starts with a quintic V with 20 double points. Let W be the surface obtained by blowing up the 20 double points. Suppose that W has a double cover X branched over the 20...
s are simply connected. - c2 = 10: Godeaux surfaceGodeaux surfaceIn mathematics, a Godeaux surface is one of the surfaces of general type introduced by Lucien Godeaux.Other surfaces constructed in a similar way with the same Hodge numbers are also sometimes called Godeaux surfaces...
s. The cyclic group of order 5 acts freely on the Fermat surface of points (w : x : y : z) in P3 satisfying w5 + x5 + y5 + z5 = 0 by mapping (w : x : y : z) to (w:ρx:ρ2y:ρ3z) where ρ is a fifth root of 1. The quotient by this action is the original Godeaux surface. Other surfaces constructed in a similar way with the same Hodge numbers are also sometimes called Godeaux surfaces. Surfaces with the same Hodge numbers (such as Barlow surfaces) are called numerical Godeaux surfaces. The fundamental group (of the original Godeaux surface) is cyclic of order 5. - c2 = 11: Barlow surfaceBarlow surfaceIn mathematics, a Barlow surface is one of the complex surfaces introduced by .They are simply connected surfaces of general type with pg = 0. They are homeomorphic but not diffeomorphic to a projective plane blown up in 8 points....
s are simply connected, and are the only known examples of simply connected surfaces of general type with pg = 0.
Other Examples
- Castelnuovo surfaceCastelnuovo surfaceIn mathematics, a Castelnuovo surface is a surface of general type such that the canonical bundle is very ample andsuch that c12 = 3pg − 7. Guido Castelnuovo proved that if the canonical bundle is very ample for a surface of general type then...
s: Another extremal case, Castelnuovo proved that if the canonical bundle is very ample for a surface of general type then c12 ≥ 3pg − 7. Castelnuovo surface are surfaces of general type such that the canonical bundle is very ample and that c12 = 3pg − 7. - Complete intersectionComplete intersectionIn mathematics, an algebraic variety V in projective space is a complete intersection if it can be defined by the vanishing of the number of homogeneous polynomials indicated by its codimension...
s: A smooth complete intersection of hypersurfaces of degrees d1 ≥ d2 ≥ ... ≥ dn−2 ≥ 2 in Pn is a surface of general type unless the degrees are (2), (3), (2, 2) (rational), (4), (3, 2), (2, 2, 2) (Kodaira dimension 0). Complete intersections are all simply connected. A special case are hypersurfaces: for example, in P3, non-singular surfaces of degree at least 5 are of general type (Non-singular hypersurfaces of degree 4 are K3 surfaceK3 surfaceIn mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s, and those of degree less than 4 are rational). - Fano surfaceFano surfaceIn algebraic geometry, a Fano surface is a surface of general type whose points index the lines on a non-singular cubic threefold...
s of lines on a cubic 3-fold. - Hilbert modular surfaceHilbert modular surfaceIn mathematics, a Hilbert modular surface is one of the surfaces obtained by taking a quotient of a product of two copies of the upper half-plane by a Hilbert modular group....
s are mostly of general type. - Horikawa surfaceHorikawa surfaceIn mathematics, a Horikawa surface is one of the surfaces of general type introduced by Horikawa.These are surfaces with q = 0 and pg = c12/2 + 2 or c12/2 + 3/2 .They are all simply connected, and Horikawa gave a...
s are surfaces with q = 0 and pg = c12/2 + 2 or c12/2 + 3/2 (which implies that they are more or less on the "Noether line" edge of the region of possible values of the Chern numbers). They are all simply connected, and Horikawa gave a detailed description of them. - Products: the product of two curves both of genus at least 2 is a surface of general type.
- Double covers of non-singular degree 2m curves in P2 are of general type if 2m≥8. (For 2m=2 they are rational, for 2m=4 they are again rational and called del Pezzo double planes, and for 2m=6 they are K3 surfaceK3 surfaceIn mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s.) They are simply connected, and have Chern numbers c12 = 2(m − 3)2, c2 = 4m2 − 6m + 6.
Canonical models
proved that the multicanonical map φnK for a complex surface of general type is a birational isomorphism onto its image whenever n≥5, and showed that the same result still holds in positive characteristic. There are some surfaces for which it is not a birational isomorphism when n is 4.These results follow from Reider's theorem
Reider's theorem
In algebraic geometry, Reider's theorem gives conditions for a line bundle on a projective surface to be very ample.-Statement:Suppose that L is a line bundle on a smooth projective surface with canonical bundle K...
.

