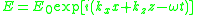Surface plasmon
Encyclopedia
Surface plasmons are coherent electron
oscillations that exist at the interface between any two materials where the real part of the dielectric function changes sign across the interface (e.g. a metal-dielectric interface, such as a metal sheet in air). SPs have lower energy than bulk (or volume) plasmon
s which quantise the longitudinal electron oscillations about positive ion cores within the bulk of an electron gas (or plasma). When SPs couple with a photon
, the resulting hybridised excitation is called a surface plasmon polariton (SPP). This SPP can propagate along the surface of a metal until energy is lost either via absorption in the metal or radiation into free-space. The existence of surface plasmons was first predicted in 1957 by R.H. Ritchie. In the following two decades, surface plasmons were extensively studied by many scientists, the foremost of whom were Heinz Raether, E. Kretschmann, and A. Otto.
Coupling of photons into SPPs can be achieved using a coupling medium such as a prism
or grating to match the photon and surface plasmon wave vectors. A prism can be positioned against a thin metal film in the Kretschmann configuration or very close to a metal surface in the Otto configuration (Figure 1). A grating coupler matches the wave vectors by increasing the parallel wave vector component by an amount related to the grating period (Figure 2). This method, while less frequently utilized, is critical to the theoretical understanding of the impact of surface roughness. Moreover, simple isolated surface defects such as a groove, a slit or a corrugation on an otherwise planar surface provides a mechanism by which free-space radiation and SPPs can exchange energy and hence couple.
where k is the wave number and ω is the frequency of the wave. By solving Maxwell's equations
for the electromagnetic wave at an interface between two materials with relative dielectric functions ε1 and ε2 (see figure 3) with the appropriate continuity relation the boundary conditions are

and
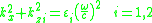
where c is the speed of light
in a vacuum, and kx is same for both media at the interface for a surface wave. Solving these two equations, the dispersion relation for a wave propagating on the surface is
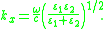
In the free electron model of an electron gas, which neglects attenuation, the metallic dielectric function is
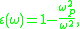
where the bulk plasma frequency in SI units is
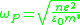
where n is the electron density, e is the charge of the electron, m* is the effective mass
of the electron and is the permittivity of free-space. The dispersion
is the permittivity of free-space. The dispersion
relation is plotted in Figure 4. At low k, the SPP behaves like a photon, but as k increases, the dispersion relation bends over and reaches an asymptotic limit corresponding to the surface plasma frequency. Since the dispersion curve lies to the right of the light line, ω = k·c, the SPP has a shorter wavelength than free-space radiation such that the out-of-plane component of the SPP is purely imaginary and exhibits evanescent decay. The surface plasma frequency is given by
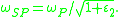
In the case of air, this result simplifies to

If we assume that ε2 is real and ε2 > 0, then it must be true that ε1 < 0, a condition which is satisfied in metals. Electromagnetic waves passing through a metal experience damping due to Ohmic losses and electron-core interactions. These effects show up in as an imaginary component of the dielectric function. The dielectric function of a metal is expressed ε1 = ε1' + i·ε1" where ε1' and ε1" are the real and imaginary parts of the dielectric function, respectively. Generally |ε1'| >> ε1" so the wavenumber can be expressed in terms of its real and imaginary components as
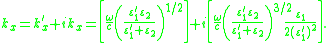
The wave vector gives us insight into physically meaningful properties of the electromagnetic wave such as its spatial extent and coupling requirements for wave vector matching.
, so at a distance x, the intensity has decreased by a factor of exp[-2kx"x]. The propagation length is defined as the distance for the SPP intensity to decay by a factor of 1/e. This condition is satisfied at a length
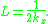
Likewise, the electric field falls off evanescently perpendicular to the metal surface. At low frequencies, the SPP penetration depth into the metal is commonly approximated using the skin depth formula. In the dielectric, the field will fall off far more slowly. The decay lengths in the metal and dielectric medium can be expressed as

where i indicates the medium of propagation. Surface plasmons are very sensitive to slight perturbations within the skin depth and because of this, surface plasmons are often used to probe inhomogeneities of a surface.
Figure2. When a photon is incident on a surface, the wave vector of the photon in the dielectric material is smaller than that of the SPP. In order for the photon to couple into a SPP, the wave vector must increase by . The grating harmonics of a periodic grating provide additional momentum parallel to the supporting interface to match the terms.
. The grating harmonics of a periodic grating provide additional momentum parallel to the supporting interface to match the terms.
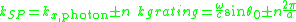
where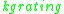 is the wave vector of the grating,
is the wave vector of the grating, 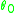 is the angle of incidence of the incoming photon, a is the grating period, and n is an integer.
is the angle of incidence of the incoming photon, a is the grating period, and n is an integer.
Rough surfaces can be thought of as the superposition
of many gratings of different periodicities. Kretschmann proposed that a statistical correlation function
be defined for a rough surface
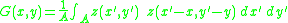
where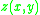 is the height above the mean surface height at the position
is the height above the mean surface height at the position 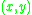 , and
, and  is the area of integration. Assuming that the statistical correlation function is Gaussian of the form
is the area of integration. Assuming that the statistical correlation function is Gaussian of the form

where is the root mean square
is the root mean square
height, is the distance from the point
is the distance from the point 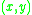 , and
, and  is the correlation length, then the Fourier transform
is the correlation length, then the Fourier transform
of the correlation function is
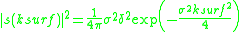
where is a measure of the amount of each spatial frequency
is a measure of the amount of each spatial frequency
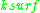 which help couple photons into a surface plasmon.
which help couple photons into a surface plasmon.
If the surface only has one Fourier component of roughness (i.e. the surface profile is sinusoidal), then the is discrete and exists only at
is discrete and exists only at 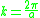 , resulting in a single narrow set of angles for coupling. If the surface contains many Fourier components, then coupling becomes possible at multiple angles. For a random surface,
, resulting in a single narrow set of angles for coupling. If the surface contains many Fourier components, then coupling becomes possible at multiple angles. For a random surface,  becomes continuous and the range of coupling angles broadens.
becomes continuous and the range of coupling angles broadens.
As stated earlier, surface plasmons are non-radiative. When a surface plasmon travels along a rough surface, it usually becomes radiative due to scattering. The Surface Scattering Theory of light suggests that the scattered intensity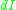 per solid angle
per solid angle
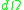 per incident intensity
per incident intensity 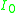 is
is
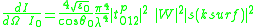
where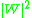 is the radiation pattern from a single dipole
is the radiation pattern from a single dipole
at the metal/dielectric interface. If surface plasmons are excited in the Kretschmann geometry and the scattered light is observed in the plane of incidence (Fig. 4), then the dipole function becomes
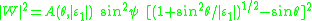
with

where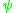 is the polarization angle and
is the polarization angle and 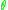 is the angle from the z-axis in the xz-plane. Two important consequences come out of these equations. The first is that if
is the angle from the z-axis in the xz-plane. Two important consequences come out of these equations. The first is that if 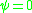 (s-polarization), then
(s-polarization), then 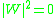 and the scattered light
and the scattered light 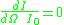 . Secondly, the scattered light has a measurable profile which is readily correlated to the roughness. This topic is treated in greater detail in reference.
. Secondly, the scattered light has a measurable profile which is readily correlated to the roughness. This topic is treated in greater detail in reference.
(SPR). In SPR, the maximum excitation of surface plasmons are detected by monitoring the reflected power from a prism coupler as a function of incident angle or wavelength
. This technique can be used to observe nanometer changes in thickness, density fluctuations, or molecular adsorption.
In surface second harmonic generation
, the second harmonic signal is proportional to the square of the electric field. The electric field is stronger at the interface because of the surface plasmon resulting in a non-linear optical effect
. This larger signal is often exploited to produce a stronger second harmonic signal.
The wavelength and intensity of the plasmon-related absorption and emission peaks are affected by molecular adsorption that can be used in molecular sensors. For example, a fully operational prototype device detecting casein in milk has been fabricated. The device is based on monitoring changes in plasmon-related absorption of light by a gold layer.
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
oscillations that exist at the interface between any two materials where the real part of the dielectric function changes sign across the interface (e.g. a metal-dielectric interface, such as a metal sheet in air). SPs have lower energy than bulk (or volume) plasmon
Plasmon
In physics, a plasmon is a quantum of plasma oscillation. The plasmon is a quasiparticle resulting from the quantization of plasma oscillations just as photons and phonons are quantizations of light and mechanical vibrations, respectively...
s which quantise the longitudinal electron oscillations about positive ion cores within the bulk of an electron gas (or plasma). When SPs couple with a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, the resulting hybridised excitation is called a surface plasmon polariton (SPP). This SPP can propagate along the surface of a metal until energy is lost either via absorption in the metal or radiation into free-space. The existence of surface plasmons was first predicted in 1957 by R.H. Ritchie. In the following two decades, surface plasmons were extensively studied by many scientists, the foremost of whom were Heinz Raether, E. Kretschmann, and A. Otto.
Excitation
Surface plasmons can be excited by both electrons and photons. Excitation by electrons is created by firing electrons into the bulk of a metal. As the electrons scatter, energy is transferred into the bulk plasma. The component of the scattering vector parallel to the surface results in the formation of a surface plasmon.Coupling of photons into SPPs can be achieved using a coupling medium such as a prism
Prism (optics)
In optics, a prism is a transparent optical element with flat, polished surfaces that refract light. The exact angles between the surfaces depend on the application. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides, and in colloquial use...
or grating to match the photon and surface plasmon wave vectors. A prism can be positioned against a thin metal film in the Kretschmann configuration or very close to a metal surface in the Otto configuration (Figure 1). A grating coupler matches the wave vectors by increasing the parallel wave vector component by an amount related to the grating period (Figure 2). This method, while less frequently utilized, is critical to the theoretical understanding of the impact of surface roughness. Moreover, simple isolated surface defects such as a groove, a slit or a corrugation on an otherwise planar surface provides a mechanism by which free-space radiation and SPPs can exchange energy and hence couple.
Dispersion relation
The electric field of a propagating electromagnetic wave can be expressedwhere k is the wave number and ω is the frequency of the wave. By solving Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for the electromagnetic wave at an interface between two materials with relative dielectric functions ε1 and ε2 (see figure 3) with the appropriate continuity relation the boundary conditions are

and
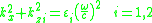
where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum, and kx is same for both media at the interface for a surface wave. Solving these two equations, the dispersion relation for a wave propagating on the surface is
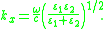
In the free electron model of an electron gas, which neglects attenuation, the metallic dielectric function is
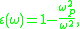
where the bulk plasma frequency in SI units is
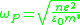
where n is the electron density, e is the charge of the electron, m* is the effective mass
Effective mass
In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
of the electron and
 is the permittivity of free-space. The dispersion
is the permittivity of free-space. The dispersionDispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
relation is plotted in Figure 4. At low k, the SPP behaves like a photon, but as k increases, the dispersion relation bends over and reaches an asymptotic limit corresponding to the surface plasma frequency. Since the dispersion curve lies to the right of the light line, ω = k·c, the SPP has a shorter wavelength than free-space radiation such that the out-of-plane component of the SPP is purely imaginary and exhibits evanescent decay. The surface plasma frequency is given by
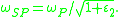
In the case of air, this result simplifies to

If we assume that ε2 is real and ε2 > 0, then it must be true that ε1 < 0, a condition which is satisfied in metals. Electromagnetic waves passing through a metal experience damping due to Ohmic losses and electron-core interactions. These effects show up in as an imaginary component of the dielectric function. The dielectric function of a metal is expressed ε1 = ε1' + i·ε1" where ε1' and ε1" are the real and imaginary parts of the dielectric function, respectively. Generally |ε1'| >> ε1" so the wavenumber can be expressed in terms of its real and imaginary components as
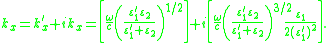
The wave vector gives us insight into physically meaningful properties of the electromagnetic wave such as its spatial extent and coupling requirements for wave vector matching.
Propagation length and skin depth
As an SPP propagates along the surface, it loses energy to the metal due to absorption. The intensity of the surface plasmon decays with the square of the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, so at a distance x, the intensity has decreased by a factor of exp[-2kx"x]. The propagation length is defined as the distance for the SPP intensity to decay by a factor of 1/e. This condition is satisfied at a length
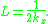
Likewise, the electric field falls off evanescently perpendicular to the metal surface. At low frequencies, the SPP penetration depth into the metal is commonly approximated using the skin depth formula. In the dielectric, the field will fall off far more slowly. The decay lengths in the metal and dielectric medium can be expressed as

where i indicates the medium of propagation. Surface plasmons are very sensitive to slight perturbations within the skin depth and because of this, surface plasmons are often used to probe inhomogeneities of a surface.
Effects of roughness
In order to understand the effect of roughness on surface plasmons, it is beneficial to first understand how a plasmon is coupled by a gratingDiffraction grating
In optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as...
Figure2. When a photon is incident on a surface, the wave vector of the photon in the dielectric material is smaller than that of the SPP. In order for the photon to couple into a SPP, the wave vector must increase by
 . The grating harmonics of a periodic grating provide additional momentum parallel to the supporting interface to match the terms.
. The grating harmonics of a periodic grating provide additional momentum parallel to the supporting interface to match the terms.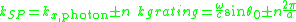
where
 is the wave vector of the grating,
is the wave vector of the grating, 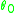 is the angle of incidence of the incoming photon, a is the grating period, and n is an integer.
is the angle of incidence of the incoming photon, a is the grating period, and n is an integer.Rough surfaces can be thought of as the superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of many gratings of different periodicities. Kretschmann proposed that a statistical correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
be defined for a rough surface
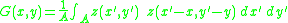
where
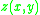 is the height above the mean surface height at the position
is the height above the mean surface height at the position 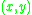 , and
, and 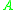 is the area of integration. Assuming that the statistical correlation function is Gaussian of the form
is the area of integration. Assuming that the statistical correlation function is Gaussian of the form
where
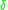 is the root mean square
is the root mean squareRoot mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
height,
 is the distance from the point
is the distance from the point 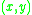 , and
, and  is the correlation length, then the Fourier transform
is the correlation length, then the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the correlation function is
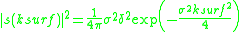
where
 is a measure of the amount of each spatial frequency
is a measure of the amount of each spatial frequencySpatial frequency
In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components of the structure repeat per unit of distance. The SI unit of spatial frequency is...
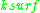 which help couple photons into a surface plasmon.
which help couple photons into a surface plasmon.If the surface only has one Fourier component of roughness (i.e. the surface profile is sinusoidal), then the
 is discrete and exists only at
is discrete and exists only at 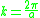 , resulting in a single narrow set of angles for coupling. If the surface contains many Fourier components, then coupling becomes possible at multiple angles. For a random surface,
, resulting in a single narrow set of angles for coupling. If the surface contains many Fourier components, then coupling becomes possible at multiple angles. For a random surface,  becomes continuous and the range of coupling angles broadens.
becomes continuous and the range of coupling angles broadens.As stated earlier, surface plasmons are non-radiative. When a surface plasmon travels along a rough surface, it usually becomes radiative due to scattering. The Surface Scattering Theory of light suggests that the scattered intensity
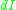 per solid angle
per solid angleSolid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
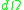 per incident intensity
per incident intensity 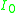 is
is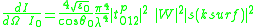
where
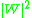 is the radiation pattern from a single dipole
is the radiation pattern from a single dipoleDipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
at the metal/dielectric interface. If surface plasmons are excited in the Kretschmann geometry and the scattered light is observed in the plane of incidence (Fig. 4), then the dipole function becomes
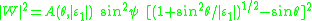
with

where
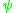 is the polarization angle and
is the polarization angle and 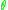 is the angle from the z-axis in the xz-plane. Two important consequences come out of these equations. The first is that if
is the angle from the z-axis in the xz-plane. Two important consequences come out of these equations. The first is that if 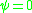 (s-polarization), then
(s-polarization), then 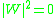 and the scattered light
and the scattered light 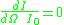 . Secondly, the scattered light has a measurable profile which is readily correlated to the roughness. This topic is treated in greater detail in reference.
. Secondly, the scattered light has a measurable profile which is readily correlated to the roughness. This topic is treated in greater detail in reference.Experimental applications
The excitation of surface plasmons is frequently used in an experimental technique known as surface plasmon resonanceSurface plasmon resonance
The excitation of surface plasmons by light is denoted as a surface plasmon resonance for planar surfaces or localized surface plasmon resonance for nanometer-sized metallic structures....
(SPR). In SPR, the maximum excitation of surface plasmons are detected by monitoring the reflected power from a prism coupler as a function of incident angle or wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. This technique can be used to observe nanometer changes in thickness, density fluctuations, or molecular adsorption.
In surface second harmonic generation
Surface second harmonic generation
Surface second harmonic generation is a method for probing interfaces in atomic and molecular systems. In second harmonic generation , the light frequency is doubled, essentially converting two photons of the original beam of energy E into a single photon of energy 2E as it interacts with...
, the second harmonic signal is proportional to the square of the electric field. The electric field is stronger at the interface because of the surface plasmon resulting in a non-linear optical effect
Nonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
. This larger signal is often exploited to produce a stronger second harmonic signal.
The wavelength and intensity of the plasmon-related absorption and emission peaks are affected by molecular adsorption that can be used in molecular sensors. For example, a fully operational prototype device detecting casein in milk has been fabricated. The device is based on monitoring changes in plasmon-related absorption of light by a gold layer.
See also
- Surface plasmon resonanceSurface plasmon resonanceThe excitation of surface plasmons by light is denoted as a surface plasmon resonance for planar surfaces or localized surface plasmon resonance for nanometer-sized metallic structures....
- Waves in plasmasWaves in plasmasWaves in plasmas are an interconnected set of particles and fields which propagates in a periodically repeating fashion. A plasma is a quasineutral, electrically conductive fluid. In the simplest case, it is composed of electrons and a single species of positive ions, but it may also contain...
- Free electron modelFree electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
- plasmonPlasmonIn physics, a plasmon is a quantum of plasma oscillation. The plasmon is a quasiparticle resulting from the quantization of plasma oscillations just as photons and phonons are quantizations of light and mechanical vibrations, respectively...
- Plasma oscillationPlasma oscillationPlasma oscillations, also known as "Langmuir waves" , are rapid oscillations of the electron density in conducting media such as plasmas or metals. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency only depends weakly on the...
- BiosensorBiosensorA biosensor is an analytical device for the detection of an analyte that combines a biological component with a physicochemical detector component.It consists of 3 parts:* the sensitive biological element A biosensor is an analytical device for the detection of an analyte that combines a biological...
- SpinplasmonicsSpinplasmonicsSpinplasmonics is a field nanotechnology combining spintronics and plasmonics. The field was pioneered by Professor Abdulhakem Elezzabi at the University of Alberta in Canada. In a simple spinplasmonic device, light waves couple to electron spin states in a metallic structure...
- extraordinary optical transmissionExtraordinary Optical TransmissionExtraordinary optical transmission is the phenomenon of greatly enhanced transmission of light through a subwavelength aperture in an otherwise opaque metallic film which has been patterned with a regularly repeating periodic structure...
- Dual Polarisation InterferometryDual Polarisation InterferometryDual polarization interferometry is an analytical technique that can probe molecular scale layers adsorbed to the surface of a waveguide by using the evanescent wave of a laser beam confined to the waveguide...