Effective mass
Encyclopedia
In solid state physics, a particle's effective mass is the mass
it seems to carry in the semiclassical model of transport in a crystal
. It can be shown that electron
s and holes
in a crystal
respond to electric
and magnetic field
s almost as if they were particles with a mass dependence in their direction of travel, an effective mass tensor
. In a simplified picture that ignores crystal anisotropies, they behave as free particles in a vacuum, but with a different mass. This mass is usually stated in units of the ordinary mass of an electron me (9.11×10−31 kg
). In these units it is usually in the range 0.01 to 10, but can also be lower or higher, for example reaching 1000 in exotic heavy fermion
materials, and reaching 0 at the so-called Dirac points in graphene
.
The effective mass has important effects on the properties of a solid, including everything from the efficiency of a solar cell to the speed of an integrated circuit.
Effective mass is defined by analogy with Newton's second law
F = m a. Using quantum mechanics
it can be shown that for an electron in an external electric field E, the acceleration aℓ along coordinate direction ℓ is:
where ћ = h/2π is reduced Planck's constant, k is the wave vector
(often loosely called momentum
since k = p / ћ for free electrons), ε (k) is the energy as a function of k, or the dispersion relation
as it is often called.
For a free particle, the dispersion relation is a quadratic, and so the effective mass would be constant (and equal to the real mass). In a crystal, the situation is far more complex. The dispersion relation is not even approximately quadratic, in the large scale. However, wherever a minimum occurs in the dispersion relation, the minimum can be approximated by a quadratic curve in the small region around that minimum, for example:
where the minimum is assumed to occur at k=0. In many semiconductors the minimum does not occur at k=0. For example, in silicon the conduction band
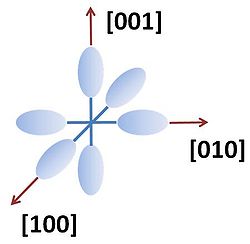
has six symmetrically located minima along the Δ = [100] symmetry lines in k-space. The constant energy surfaces at these minima are ellipsoids oriented along the k-space axes (see figure).
In contrast, the holes
at the top of the silicon valence band are classified as light and heavy and the band energies for the two types are given by a complicated relation:
leading to what is termed warped energy surfaces. Parameters A, B and C are wavevector independent constants. This behavior is introduced here to alert the reader that it is common for carriers to have rather non-parabolic energy-wavevector relations.
A simplification can be made, however, for electrons which have energy close to a minimum, and where the effective mass is the same in all directions, the mass can be approximated as a scalar
:
In energy regions far away from a minimum, effective mass can be negative or even approach infinity
. Effective mass, being generally dependent on direction (with respect to the crystal axes
), is a tensor
. However, for many calculations the various directions can be averaged out.
Effective mass should not be confused with reduced mass
, which is a concept from Newtonian mechanics
. Effective mass can be understood only with quantum mechanics.
. For a wave packet the group velocity is given by:
= 
Now we can say:
where p is the electron's momentum. Substitute the expression for the group velocity into this last equation and we get:
From this follows the definition of effective mass:
An alternative derivation can be given by considering the Hamiltonian of a free particle and using the de Broglie relation
:
The same result is obtained, identifying the Hamiltonian with the total energy:
. These masses are related, but are not the same because the weighting of various directions and wavevectors are different. The density-of-states effective masses are tabulated below for a few cases.
, a method in which microwave absorption of a semiconductor immersed in a magnetic field goes through a sharp peak when the microwave frequency equals the cyclotron frequency
. In recent years effective masses have more commonly been determined through measurement of band structures using techniques such as angle-resolved photo emission
(ARPES) or, most directly, the de Haas-van Alphen effect
. Effective masses can also be estimated using the coefficient γ of the linear term in the low-temperature electronic specific heat at constant volume
. The specific heat depends on the effective mass through the density of states at the Fermi level and as such is a measure of degeneracy as well as band curvature. Very large estimates of carrier mass from specific heat measurements have given rise to the concept of heavy fermion
materials. Since carrier mobility
depends on the ratio of carrier collision lifetime
to effective mass, masses can in principle be determined from transport measurements, but this method is not practical since carrier collision probabilities are typically not known a priori.
of electronic transport, the maximum obtainable charge carrier velocity is inversely proportional to the effective mass:
where 
with 
being the electronic charge
. The ultimate speed of integrated circuit
s depends on the carrier velocity, so the low effective mass is the fundamental reason that GaAs and its derivatives are used instead of Si in high-bandwidth applications like cellular telephony.
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
it seems to carry in the semiclassical model of transport in a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
. It can be shown that electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s and holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
in a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
respond to electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s almost as if they were particles with a mass dependence in their direction of travel, an effective mass tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. In a simplified picture that ignores crystal anisotropies, they behave as free particles in a vacuum, but with a different mass. This mass is usually stated in units of the ordinary mass of an electron me (9.11×10−31 kg
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
). In these units it is usually in the range 0.01 to 10, but can also be lower or higher, for example reaching 1000 in exotic heavy fermion
Heavy Fermion
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons. Electrons, a kind of fermion, found in such materials are sometimes referred to as heavy electrons...
materials, and reaching 0 at the so-called Dirac points in graphene
Graphene
Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer...
.
The effective mass has important effects on the properties of a solid, including everything from the efficiency of a solar cell to the speed of an integrated circuit.
Definition
When an electron is moving inside a solid material, the force between other atoms will affect its movement and it will not be described by Newton's law. So we introduce the concept of effective mass to describe the movement of electron in Newton's law. The effective mass can be negative or different due to circumstances. Generally, in the absence of an electric or magnetic field, the concept of effective mass does not apply.Effective mass is defined by analogy with Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
F = m a. Using quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
it can be shown that for an electron in an external electric field E, the acceleration aℓ along coordinate direction ℓ is:
where ћ = h/2π is reduced Planck's constant, k is the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
(often loosely called momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
since k = p / ћ for free electrons), ε (k) is the energy as a function of k, or the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
as it is often called.
For a free particle, the dispersion relation is a quadratic, and so the effective mass would be constant (and equal to the real mass). In a crystal, the situation is far more complex. The dispersion relation is not even approximately quadratic, in the large scale. However, wherever a minimum occurs in the dispersion relation, the minimum can be approximated by a quadratic curve in the small region around that minimum, for example:
where the minimum is assumed to occur at k=0. In many semiconductors the minimum does not occur at k=0. For example, in silicon the conduction band
Conduction band
In the solid-state physics field of semiconductors and insulators, the conduction band is the range of electron energies, higher than that of the valence band, sufficient to free an electron from binding with its individual atom and allow it to move freely within the atomic lattice of the material...
has six symmetrically located minima along the Δ = [100] symmetry lines in k-space. The constant energy surfaces at these minima are ellipsoids oriented along the k-space axes (see figure).
In contrast, the holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
at the top of the silicon valence band are classified as light and heavy and the band energies for the two types are given by a complicated relation:
leading to what is termed warped energy surfaces. Parameters A, B and C are wavevector independent constants. This behavior is introduced here to alert the reader that it is common for carriers to have rather non-parabolic energy-wavevector relations.
A simplification can be made, however, for electrons which have energy close to a minimum, and where the effective mass is the same in all directions, the mass can be approximated as a scalar
:In energy regions far away from a minimum, effective mass can be negative or even approach infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. Effective mass, being generally dependent on direction (with respect to the crystal axes
Miller index
Miller indices form a notation system in crystallography for planes and directions in crystal lattices.In particular, a family of lattice planes is determined by three integers h, k, and ℓ, the Miller indices. They are written , and each index denotes a plane orthogonal to a direction in the...
), is a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. However, for many calculations the various directions can be averaged out.
Effective mass should not be confused with reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
, which is a concept from Newtonian mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
. Effective mass can be understood only with quantum mechanics.
Derivation
In the free electron model, the electronic wave function is given by. For a wave packet the group velocity is given by: = Now we can say:
where p is the electron's momentum. Substitute the expression for the group velocity into this last equation and we get:
From this follows the definition of effective mass:
An alternative derivation can be given by considering the Hamiltonian of a free particle and using the de Broglie relation
De Broglie hypothesis
In quantum mechanics, a matter wave or de Broglie wave is the wave of matter. The de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle and that the frequency is directly proportional to the particle's kinetic energy...
:
The same result is obtained, identifying the Hamiltonian with the total energy:
Effective mass for some common semiconductors
The effective mass is used in transport calculations, such as transport of electrons under the influence of fields or carrier gradients, but also is used to calculate the density of statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
. These masses are related, but are not the same because the weighting of various directions and wavevectors are different. The density-of-states effective masses are tabulated below for a few cases.
| Material | Electron effective mass | Hole effective mass |
|---|---|---|
| Group IV | ||
| Si Silicon Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table... (4.2K) | 1.08 me | 0.56 me |
| Ge Germanium Germanium is a chemical element with the symbol Ge and atomic number 32. It is a lustrous, hard, grayish-white metalloid in the carbon group, chemically similar to its group neighbors tin and silicon. The isolated element is a semiconductor, with an appearance most similar to elemental silicon.... | 0.55 me | 0.37 me |
| III-V | ||
| GaAs | 0.067 me | 0.45 me |
| InSb | 0.013 me | 0.6 me |
| II-VI | ||
| ZnO | 0.19 me | 1.21 me |
| ZnSe | 0.17me | 1.44 me |
Experimental determination
Traditionally effective masses were measured using cyclotron resonanceElectron cyclotron resonance
Electron cyclotron resonance is a phenomenon observed both in plasma physics and condensed matter physics. An electron in a static and uniform magnetic field will move in a circle due to the Lorentz force...
, a method in which microwave absorption of a semiconductor immersed in a magnetic field goes through a sharp peak when the microwave frequency equals the cyclotron frequency
. In recent years effective masses have more commonly been determined through measurement of band structures using techniques such as angle-resolved photo emissionPhotoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
(ARPES) or, most directly, the de Haas-van Alphen effect
De Haas-van Alphen effect
The de Haas–van Alphen effect, often abbreviated to dHvA, is a quantum mechanical effect in which the magnetic moment of a pure metal crystal oscillates as the intensity of an applied magnetic field B is increased. Other quantities also oscillate, such as the resistivity , specific heat, and sound...
. Effective masses can also be estimated using the coefficient γ of the linear term in the low-temperature electronic specific heat at constant volume
. The specific heat depends on the effective mass through the density of states at the Fermi level and as such is a measure of degeneracy as well as band curvature. Very large estimates of carrier mass from specific heat measurements have given rise to the concept of heavy fermionHeavy Fermion
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons. Electrons, a kind of fermion, found in such materials are sometimes referred to as heavy electrons...
materials. Since carrier mobility
Electron mobility
In solid-state physics, the electron mobility characterizes how quickly an electron can move through a metal or semiconductor, when pulled by an electric field. In semiconductors, there is an analogous quantity for holes, called hole mobility...
depends on the ratio of carrier collision lifetime
to effective mass, masses can in principle be determined from transport measurements, but this method is not practical since carrier collision probabilities are typically not known a priori.Significance
As the table shows, III-V compounds based on GaAs and InSb have far smaller effective masses than tetrahedral group IV materials like Si and Ge. In the simplest Drude pictureDrude model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...
of electronic transport, the maximum obtainable charge carrier velocity is inversely proportional to the effective mass:
where with being the electronic chargeElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. The ultimate speed of integrated circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
s depends on the carrier velocity, so the low effective mass is the fundamental reason that GaAs and its derivatives are used instead of Si in high-bandwidth applications like cellular telephony.
See also
- Band structure
- k·p perturbation theoryK·p perturbation theoryIn solid-state physics, k·p perturbation theory is an approximation scheme for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method"...
- SemiconductorSemiconductorA semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
- Electrical conduction
- Valence bandValence bandIn solids, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature....
- Kronig-Penney model
- Tight-binding model
- Density of statesDensity of statesIn solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...