K·p perturbation theory
Encyclopedia
In solid-state physics
, k·p perturbation theory
is an approximation scheme for calculating the band structure (particularly effective mass
) and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method". This theory has been applied specifically in the framework of the Luttinger–Kohn model (after Joaquin Mazdak Luttinger
and Walter Kohn
), and of the Kane model (after Evan O. Kane).
(in the single-electron approximation
), the electron
s in any material have wavefunction
s which can be described by the following Schrödinger equation
:
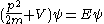
where p is the quantum-mechanical momentum operator
, V is the potential, and m is the mass of an electron. (This equation neglects the spin-orbit effect; see below.)
In a crystalline solid, V is a periodic function
, with the same periodicity as the crystal lattice. Bloch's theorem
proves that the solutions to this differential equation can be written as follows: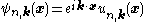
where k is a vector (called the wavevector), n is a discrete index (called the band index), and un,k is a function with the same periodicity as the crystal lattice.
For any given n, the associated states are called a band. In each band, there will be a relation between the wavevector k and the energy of the state En,k, called the band dispersion
. Calculating this dispersion is one of the primary applications of k·p perturbation theory.
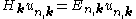
where the Hamiltonian
is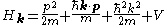
Note that k is a vector consisting of three real numbers with units of inverse length, while p is a vector of operators; to be explicit,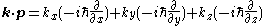
In any case, we write this Hamiltonian as the sum of two terms: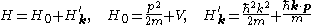
This expression is the basis for perturbation theory
. The "unperturbed Hamiltonian" is H0, which in fact equals the exact Hamiltonian at k=0 (i.e., at the Gamma point). The "perturbation" is the term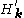
. The analysis that results is called "k·p perturbation theory", due to the term proportional to k·p. The result of this analysis is an expression for En,k and un,k in terms of the energies and wavefunctions at k=0.
Note that the "perturbation" term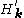
gets progressively smaller as k approaches zero. Therefore, k·p perturbation theory is most accurate for small values of k. However, if enough terms are included in the perturbative expansion
, then the theory can in fact be reasonably accurate for any value of k in the entire Brillouin zone
.
):
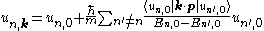
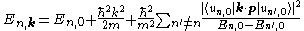
The parameters that are required to do these calculations, namely En,0 and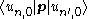
, are typically inferred from experimental data. (The latter are called "optical matrix elements".)
In practice, the sum over n often includes only the nearest one or two bands, since these tend to be the most important (due to the denominator). However, for improved accuracy, especially at larger k, more bands must be included, as well as more terms in the perturbative expansion than the ones written above.
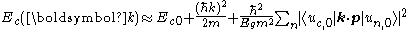
The effective mass in direction ℓ is then: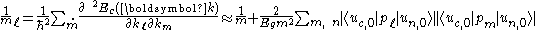
Ignoring the details of the matrix elements, the key consequences are that the effective mass varies with the smallest bandgap and goes to zero as the gap goes to zero. A useful approximation for the matrix elements in direct gap semiconductors is:
which applies within about 15% or better to most group-IV, II-V and II-VI semiconductors.
In contrast to this simple approximation, in the case of valence band energy the spin-orbit interaction must be introduced (see below) and many more bands must be individually considered. The calculation is provided in Yu and Cardona. In the valence band the mobile carriers are holes
. One finds there are two types of hole, named heavy and light, with anisotropic masses.
, the Schrödinger equation for u is: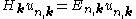
where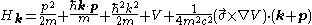
where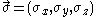
is a vector consisting of the three Pauli matrices. This Hamiltonian can be subjected to the same sort of perturbation-theory analysis as above.
s in certain materials such as gallium arsenide, the equations can be analyzed by the methods of degenerate perturbation theory
. Models of this type include the "Luttinger-Kohn model" (a.k.a. "Kohn-Luttinger model"), and the "Kane model".
Band properties
Wavefunctions
Fundamental theory
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, k·p perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
is an approximation scheme for calculating the band structure (particularly effective mass
Effective mass
In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
) and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method". This theory has been applied specifically in the framework of the Luttinger–Kohn model (after Joaquin Mazdak Luttinger
Joaquin Mazdak Luttinger
Joaquin Mazdak Luttinger was an American physicist well-known for his contributions to the theory of interacting electrons in one-dimensional metals and the Fermi-liquid theory...
and Walter Kohn
Walter Kohn
Walter Kohn is an Austrian-born American theoretical physicist.He was awarded, with John Pople, the Nobel Prize in chemistry in 1998. The award recognized their contributions to the understandings of the electronic properties of materials...
), and of the Kane model (after Evan O. Kane).
Bloch's theorem and wavevectors
According to quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(in the single-electron approximation
Hartree-Fock
In computational physics and chemistry, the Hartree–Fock method is an approximate method for the determination of the ground-state wave function and ground-state energy of a quantum many-body system....
), the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in any material have wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s which can be described by the following Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
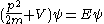
where p is the quantum-mechanical momentum operator
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, V is the potential, and m is the mass of an electron. (This equation neglects the spin-orbit effect; see below.)
In a crystalline solid, V is a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
, with the same periodicity as the crystal lattice. Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
proves that the solutions to this differential equation can be written as follows:
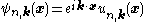
where k is a vector (called the wavevector), n is a discrete index (called the band index), and un,k is a function with the same periodicity as the crystal lattice.
For any given n, the associated states are called a band. In each band, there will be a relation between the wavevector k and the energy of the state En,k, called the band dispersion
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
. Calculating this dispersion is one of the primary applications of k·p perturbation theory.
Perturbation theory
The periodic function un,k satisfies the following Schrödinger-type equation: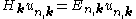where the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is
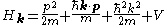
Note that k is a vector consisting of three real numbers with units of inverse length, while p is a vector of operators; to be explicit,
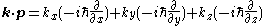
In any case, we write this Hamiltonian as the sum of two terms:
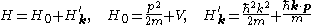
This expression is the basis for perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. The "unperturbed Hamiltonian" is H0, which in fact equals the exact Hamiltonian at k=0 (i.e., at the Gamma point). The "perturbation" is the term
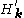. The analysis that results is called "k·p perturbation theory", due to the term proportional to k·p. The result of this analysis is an expression for En,k and un,k in terms of the energies and wavefunctions at k=0.Note that the "perturbation" term
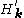gets progressively smaller as k approaches zero. Therefore, k·p perturbation theory is most accurate for small values of k. However, if enough terms are included in the perturbative expansionPerturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
, then the theory can in fact be reasonably accurate for any value of k in the entire Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
.
Expression for a nondegenerate band
For a nondegenerate band (i.e., a band which has a different energy at k=0 from any other band), with an extremum at k=0, and with no spin-orbit coupling, the result of k·p perturbation theory is (to lowest nontrivial orderPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
):
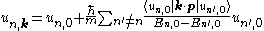
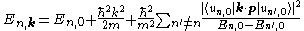
The parameters that are required to do these calculations, namely En,0 and
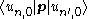, are typically inferred from experimental data. (The latter are called "optical matrix elements".)In practice, the sum over n often includes only the nearest one or two bands, since these tend to be the most important (due to the denominator). However, for improved accuracy, especially at larger k, more bands must be included, as well as more terms in the perturbative expansion than the ones written above.
Effective mass
Using the expression above for the energy dispersion relation, a simplified expression for the effective mass in the conduction band of a semiconductor can be found. To approximate the dispersion relation in the case of the conduction band, take the energy En0 as the minimum conduction band energy Ec0 and include in the summation only terms with energies near the valence band maximum, where the energy difference in the denominator is smallest. (These terms are the largest contributions to the summation.) This denominator is then approximated as the band gap Eg, leading to an energy expression: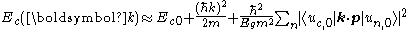The effective mass in direction ℓ is then:
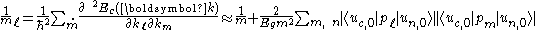
Ignoring the details of the matrix elements, the key consequences are that the effective mass varies with the smallest bandgap and goes to zero as the gap goes to zero. A useful approximation for the matrix elements in direct gap semiconductors is:
which applies within about 15% or better to most group-IV, II-V and II-VI semiconductors.
In contrast to this simple approximation, in the case of valence band energy the spin-orbit interaction must be introduced (see below) and many more bands must be individually considered. The calculation is provided in Yu and Cardona. In the valence band the mobile carriers are holes
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
. One finds there are two types of hole, named heavy and light, with anisotropic masses.
k·p model with spin-orbit interaction
Including the spin-orbit interactionSpin-orbit interaction
In quantum physics, the spin-orbit interaction is any interaction of a particle's spin with its motion. The first and best known example of this is that spin-orbit interaction causes shifts in an electron's atomic energy levels due to electromagnetic interaction between the electron's spin and...
, the Schrödinger equation for u is:
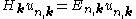
where
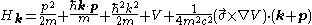
where
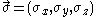is a vector consisting of the three Pauli matrices. This Hamiltonian can be subjected to the same sort of perturbation-theory analysis as above.Calculation in degenerate case
For degenerate or nearly-degenerate bands, in particular the valence bandValence band
In solids, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature....
s in certain materials such as gallium arsenide, the equations can be analyzed by the methods of degenerate perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. Models of this type include the "Luttinger-Kohn model" (a.k.a. "Kohn-Luttinger model"), and the "Kane model".
See also
Electronic band structure- Electronic band structureElectronic band structureIn solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
- Nearly-free electron modelNearly-free electron modelIn solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
- Kronig-Penney model
Band properties
- Band gapBand gapIn solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
- Effective massEffective massIn solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
- Density of statesDensity of statesIn solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
- Fermi surfaceFermi surfaceIn condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
Wavefunctions
- Wannier functions
- Bloch waves
Fundamental theory
- Kohn-Sham equationsKohn-Sham equationsIn quantum chemistry, specifically density functional theory, the Kohn–Sham equation is the Schrödinger equation of a fictitious system of non-interacting particles that generate the same density as any given system of interacting particles...
- Local-density approximationLocal-density approximationLocal-density approximations are a class of approximations to the exchange-correlation energy functional in density functional theory that depend solely upon the value of the electronic density at each point in space . Many approaches can yield local approximations to the XC energy...