Nearly-free electron model
Encyclopedia
In solid-state physics
, the nearly-free electron model (or NFE model) is a quantum mechanical
model of physical properties of electron
s that can move almost freely through the crystal lattice
of a solid. The model is closely related to the more conceptual Empty Lattice Approximation
. The model enables understanding and calculating the electronic band structure
of especially metal
s.
are traveling plane waves. Generally the time independent part of their wave function is expressed as
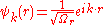
These plane wave solutions have an energy of
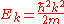
The expression of the plane wave as a complex exponential function can also be written as the sum of two periodic functions which are mutually shifted a quarter of a period.
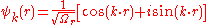
In this light the wave function of a free electron can be viewed as an aggregate of two plane waves. Sine and cosine functions can also be expressed as sums or differences of plane waves moving in opposite directions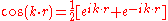
Assume that there is only one kind of atom present in the lattice and that the atoms are located at the origin of the unit cells of the lattice. The potential of the atoms is attractive and limited to a relatively small part of the volume of the unit cell of the lattice. In the remainder of the cell the potential is constant, it is zero.
The Hamiltonian
is expressed as
in which
is the kinetic and 
is the potential energy. From this expression the energy expectation value, or the statistical average, of the energy of the electron can be calculated with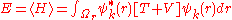
If we assume that the electron still has a free electron plane wave wave function the energy of the electron is:
Let's assume further that at a arbitrary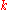
-point in the Brillouin zone we can integrate the 
over a single lattice cell, then for an arbitrary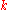 
-point the energy becomes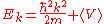
This means that at an arbitrary point the energy is lowered by the lowered average of the potential in the unit cell due to the presence of the attractive potential of the atom. If the potential is very small we get the Empty Lattice Approximation
. This isn't a very sensational result and it doesn't say anything about what happens when we get close to the Brillouin zone boundary. We will look at those regions in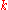
-space now.
Let's assume that we look at the problem from the origin, at position
. If 
only the cosine part is present and the sine part is moved to 
. If we let the length of the wave vector 
grow, then the central maximum of the cosine part stays at 
. The first maximum and minimum of the sine part are at 
. They come nearer as 
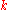grows. Let's assume that 
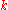is close to the Brillouin zone
boundary for the analysis in the next part of this introduction.
The atomic positions coincide with the maximum of the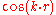
-component of the wave function. The interaction of the 
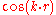-component of the wave function with the potential will be different than the interaction of the 
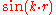-component of the wave function with the potential because their phases are shifted. The charge density is proportional to the absolute square of the wave function. For the 
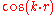-component it is
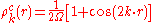
and for the
-component it is
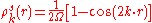
For values of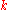
close to the Brillouin zone boundary, the length of the two waves and the period of the two different charge density distributions almost coincide with the periodic potential of the lattice. As a result the charge densities of the two components have a different energy because the maximum of the charge density of the 
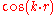-component coincides with the attractive potential of the atoms while the maximum of the charge density of the 
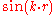-component lies in the regions with a higher electrostatic potential between the atoms.
As a result the aggregate will be split in high and low energy components when the kinetic energy increases and the wave vector approaches the length of the reciprocal lattice vectors. The potentials of the atomic cores can be decomposed into Fourier components to meet the requirements of a description in terms of reciprocal space parameters.
model which includes a weak periodic
perturbation
meant to model the interaction between the conduction electrons and the ions in a crystalline solid. This model, like the free-electron model, does not take into account electron-electron interactions; that is, the independent-electron approximation is still in effect.
As shown by Bloch's theorem
, introducing a periodic potential into the Schrödinger equation
results in a wave function of the form
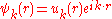
where the function u has the same periodicity as the lattice
:
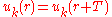
(where T is a lattice translation vector.)
Because it is a nearly free electron approximation we can assume that
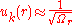
A solution of this form can be plugged into the Schrödinger equation, resulting in the central equation:
where the kinetic energy is
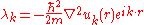
which results in
if we assume that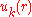
is almost constant and 
.
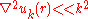The reciprocal parameters Ck and UG are the Fourier
coefficients of the wave function ψ(r) and the screened potential
energy U(r), respectively:
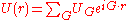
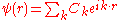
The vectors G are the reciprocal lattice vectors
, and the discrete values of k are determined by the boundary conditions of the lattice under consideration.
In any perturbation analysis, one must consider the base case to which the perturbation is applied. Here, the base case is with U(x) = 0, and therefore all the Fourier coefficients of the potential are also zero. In this case the central equation reduces to the form
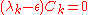
This identity means that for each k, one of the two following cases must hold:
If the values of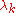
are non-degenerate
, then the second case occurs for only one value of k, while for the rest, the Fourier expansion coefficient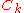
must be zero. In this non-degenerate case, the standard free electron gas result is retrieved:
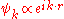
In the degenerate case, however, there will be a set of lattice vectors k1, ..., km with λ1 = ... = λm. When the energy
is equal to this value of λ, there will be m independent plane wave solutions of which any linear combination is also a solution:
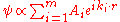
Non-degenerate and degenerate perturbation theory can be applied in these two cases to solve for the Fourier coefficients Ck of the wavefunction (correct to first order in U) and the energy eigenvalue (correct to second order in U). An important result of this derivation is that there is no first-order shift in the energy ε in the case of no degeneracy, while there is in the case of near-degeneracy, implying that the latter case is more important in this analysis. Particularly, at the Brillouin zone
boundary (or, equivalently, at any point on a Bragg plane), one finds a twofold energy degeneracy that results in a shift in energy given by:
This energy gap between Brillouin zones is known as the band gap
, with a magnitude of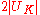
.
, most significantly resulting in a band gap
between wave vector
s in different Brillouin zone
s.
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, the nearly-free electron model (or NFE model) is a quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
model of physical properties of electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s that can move almost freely through the crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
of a solid. The model is closely related to the more conceptual Empty Lattice Approximation
Empty Lattice Approximation
The Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
. The model enables understanding and calculating the electronic band structure
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
of especially metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s.
Introduction
Free electronsFree electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
are traveling plane waves. Generally the time independent part of their wave function is expressed as
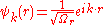
These plane wave solutions have an energy of
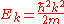
The expression of the plane wave as a complex exponential function can also be written as the sum of two periodic functions which are mutually shifted a quarter of a period.
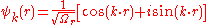
In this light the wave function of a free electron can be viewed as an aggregate of two plane waves. Sine and cosine functions can also be expressed as sums or differences of plane waves moving in opposite directions
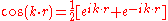
Assume that there is only one kind of atom present in the lattice and that the atoms are located at the origin of the unit cells of the lattice. The potential of the atoms is attractive and limited to a relatively small part of the volume of the unit cell of the lattice. In the remainder of the cell the potential is constant, it is zero.
The Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is expressed as
in which
is the kinetic and is the potential energy. From this expression the energy expectation value, or the statistical average, of the energy of the electron can be calculated with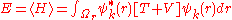If we assume that the electron still has a free electron plane wave wave function the energy of the electron is:
Let's assume further that at a arbitrary
-point in the Brillouin zone we can integrate the over a single lattice cell, then for an arbitrary 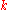-point the energy becomes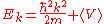This means that at an arbitrary point the energy is lowered by the lowered average of the potential in the unit cell due to the presence of the attractive potential of the atom. If the potential is very small we get the Empty Lattice Approximation
Empty Lattice Approximation
The Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
. This isn't a very sensational result and it doesn't say anything about what happens when we get close to the Brillouin zone boundary. We will look at those regions in
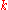-space now.Let's assume that we look at the problem from the origin, at position
. If only the cosine part is present and the sine part is moved to . If we let the length of the wave vector grow, then the central maximum of the cosine part stays at . The first maximum and minimum of the sine part are at . They come nearer as 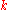grows. Let's assume that 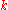is close to the Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
boundary for the analysis in the next part of this introduction.
The atomic positions coincide with the maximum of the
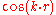-component of the wave function. The interaction of the 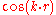-component of the wave function with the potential will be different than the interaction of the 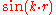-component of the wave function with the potential because their phases are shifted. The charge density is proportional to the absolute square of the wave function. For the 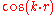-component it is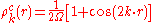and for the
-component it is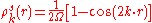For values of
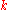close to the Brillouin zone boundary, the length of the two waves and the period of the two different charge density distributions almost coincide with the periodic potential of the lattice. As a result the charge densities of the two components have a different energy because the maximum of the charge density of the 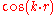-component coincides with the attractive potential of the atoms while the maximum of the charge density of the 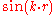-component lies in the regions with a higher electrostatic potential between the atoms.As a result the aggregate will be split in high and low energy components when the kinetic energy increases and the wave vector approaches the length of the reciprocal lattice vectors. The potentials of the atomic cores can be decomposed into Fourier components to meet the requirements of a description in terms of reciprocal space parameters.
Mathematical formulation
The nearly-free electron model is a modification of the free-electron gasFree electron model
In solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
model which includes a weak periodic
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
perturbation
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
meant to model the interaction between the conduction electrons and the ions in a crystalline solid. This model, like the free-electron model, does not take into account electron-electron interactions; that is, the independent-electron approximation is still in effect.
As shown by Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
, introducing a periodic potential into the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
results in a wave function of the form
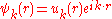
where the function u has the same periodicity as the lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
:
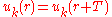
(where T is a lattice translation vector.)
Because it is a nearly free electron approximation we can assume that
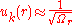
A solution of this form can be plugged into the Schrödinger equation, resulting in the central equation:
where the kinetic energy is
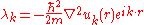
which results in
if we assume that
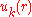is almost constant and 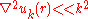.The reciprocal parameters Ck and UG are the Fourier
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
coefficients of the wave function ψ(r) and the screened potential
Screening effect
In solids, especially in metals and semiconductors, the electrostatic screening or screening effect reduces the electrostatic field and Coulomb potential of an ion inside the solid...
energy U(r), respectively:
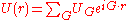
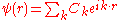
The vectors G are the reciprocal lattice vectors
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
, and the discrete values of k are determined by the boundary conditions of the lattice under consideration.
In any perturbation analysis, one must consider the base case to which the perturbation is applied. Here, the base case is with U(x) = 0, and therefore all the Fourier coefficients of the potential are also zero. In this case the central equation reduces to the form
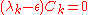
This identity means that for each k, one of the two following cases must hold:
,
If the values of
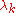are non-degenerateDegenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
, then the second case occurs for only one value of k, while for the rest, the Fourier expansion coefficient
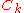must be zero. In this non-degenerate case, the standard free electron gas result is retrieved: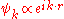In the degenerate case, however, there will be a set of lattice vectors k1, ..., km with λ1 = ... = λm. When the energy
is equal to this value of λ, there will be m independent plane wave solutions of which any linear combination is also a solution: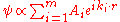Non-degenerate and degenerate perturbation theory can be applied in these two cases to solve for the Fourier coefficients Ck of the wavefunction (correct to first order in U) and the energy eigenvalue (correct to second order in U). An important result of this derivation is that there is no first-order shift in the energy ε in the case of no degeneracy, while there is in the case of near-degeneracy, implying that the latter case is more important in this analysis. Particularly, at the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
boundary (or, equivalently, at any point on a Bragg plane), one finds a twofold energy degeneracy that results in a shift in energy given by:
This energy gap between Brillouin zones is known as the band gap
Band gap
In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
, with a magnitude of
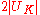.Results
Introducing this weak perturbation has significant effects on the solution to the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, most significantly resulting in a band gap
Band gap
In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
between wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
s in different Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
s.
Justifications
In this model, the assumption is made that the interaction between the conduction electrons and the ion cores can be modeled through the use of a "weak" perturbing potential. This may seem like a severe approximation, for the Coulomb attraction between these two particles of opposite charge can be quite significant at short distances. It can be partially justified, however, by noting two important properties of the quantum mechanical system:- The force between the ions and the electrons is greatest at very small distances. However, the conduction electrons are not "allowed" to get this close to the ion cores due to the Pauli exclusion principlePauli exclusion principleThe Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
: the orbitals closest to the ion core are already occupied by the core electrons. Therefore, the conduction electrons never get close enough to the ion cores to feel their full force. - Furthermore, the core electrons shieldShielding effectThe shielding effect describes the decrease in attraction between an electron and the nucleus in any atom with more than one electron shell. It is also referred to as the screening effect or atomic shielding.-Cause:...
the ion charge magnitude "seen" by the conduction electrons. The result is an effective nuclear charge experienced by the conduction electrons which is significantly reduced from the actual nuclear charge.
See also
- Empty Lattice ApproximationEmpty Lattice ApproximationThe Empty Lattice Approximation is a theoretical electronic band structure model in which the potential is defined not more precisely than periodic and weak. The Empty Lattice Approximation describes a number of properties of energy dispersion relations of non-interacting free electrons that move...
- Electronic band structureElectronic band structureIn solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
- Tight binding model
- Bloch waves
- Kronig-Penney model