Fermi surface
Encyclopedia
In condensed matter physics
, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metal
s, semimetals, and doped semiconductor
s. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands
. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle
, which allows a maximum of one electron per quantum state.
of particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy
particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy  is given by
is given by

where,
Suppose we consider the limit . Then we have,
. Then we have,

By the Pauli exclusion principle
, no two particles can be in the same state. Therefore, in the state of lowest energy, the particles fill up all energy levels till , which is equivalent to saying that
, which is equivalent to saying that  is the energy level below which there are exactly
is the energy level below which there are exactly  states.
states.
In momentum space, these particles fill up a sphere of radius , the surface of which is called the Fermi surface
, the surface of which is called the Fermi surface
The linear response of a metal to an electric, magnetic or thermal gradient is determined by the shape of the Fermi surface, because currents are due to changes in the occupancy of states near the Fermi energy. Free-electron Fermi surfaces are spheres of radius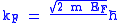 determined by the valence electron concentration where
determined by the valence electron concentration where  is the reduced Planck's constant. A material whose Fermi level falls in a gap between bands is an insulator
is the reduced Planck's constant. A material whose Fermi level falls in a gap between bands is an insulator
or semiconductor depending on the size of the bandgap. When a material's Fermi level falls in a bandgap, there is no Fermi surface.
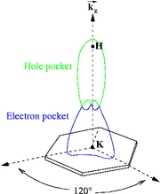
 Materials with complex crystal structures can have quite intricate Fermi surfaces. The figure illustrates the anisotropic Fermi surface of graphite, which has both electron and hole pockets in its Fermi surface due to multiple bands crossing the Fermi energy along the
Materials with complex crystal structures can have quite intricate Fermi surfaces. The figure illustrates the anisotropic Fermi surface of graphite, which has both electron and hole pockets in its Fermi surface due to multiple bands crossing the Fermi energy along the  direction. Often in a metal the Fermi surface radius
direction. Often in a metal the Fermi surface radius  is larger than the size of the first Brillouin zone
is larger than the size of the first Brillouin zone
which results in a portion of the Fermi surface lying in the second (or higher) zones. As with the band structure itself, the Fermi surface can be displayed in an extended-zone scheme where is allowed to have arbitrarily large values or a reduced-zone scheme where wavevectors are shown modulo
is allowed to have arbitrarily large values or a reduced-zone scheme where wavevectors are shown modulo
 (in the 1-dimensional case) where a is the lattice constant
(in the 1-dimensional case) where a is the lattice constant
. In the three dimensional case the reduced zone scheme means that from any wavevector there is an appropriate number of reciprocal lattice vectors
there is an appropriate number of reciprocal lattice vectors  subtracted that the new
subtracted that the new  now is closer to the origin in
now is closer to the origin in  -space than to any
-space than to any  . Solids with a large density of states at the Fermi level become unstable at low temperatures and tend to form ground state
. Solids with a large density of states at the Fermi level become unstable at low temperatures and tend to form ground state
s where the condensation energy comes from opening a gap at the Fermi surface. Examples of such ground states are superconductors, ferromagnets, Jahn–Teller distortions and spin density wave
s.
The state occupancy of fermion
s like electrons is governed by Fermi–Dirac statistics so at finite temperatures the Fermi surface is accordingly broadened. In principle all fermion energy level populations are bound by a Fermi surface although the term is not generally used outside of condensed-matter physics.
 , for example the de Haas-van Alphen effect
, for example the de Haas-van Alphen effect
(dHvA) and the Shubnikov–de Haas effect (SdH). The former is an oscillation in magnetic susceptibility
and the latter in resistivity
. The oscillations are periodic versus and occur because of the quantization of energy levels in the plane perpendicular to a magnetic field, a phenomenon first predicted by Lev Landau
and occur because of the quantization of energy levels in the plane perpendicular to a magnetic field, a phenomenon first predicted by Lev Landau
. The new states are called Landau levels and are separated by an energy where
where 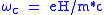 is called the cyclotron frequency
is called the cyclotron frequency
, is the electronic charge,
is the electronic charge, 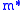 is the electron effective mass and
is the electron effective mass and  is the speed of light
is the speed of light
. In a famous result, Lars Onsager
proved that the period of oscillation is related to the cross-section of the Fermi surface (typically given in
is related to the cross-section of the Fermi surface (typically given in 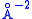 ) perpendicular to the magnetic field direction
) perpendicular to the magnetic field direction 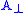 by the equation
by the equation  . Thus the determination of the periods of oscillation for various applied field directions allows mapping of the Fermi surface.
. Thus the determination of the periods of oscillation for various applied field directions allows mapping of the Fermi surface.
Observation of the dHvA and SdH oscillations requires magnetic fields large enough that the circumference of the cyclotron orbit is smaller than a mean free path
. Therefore dHvA and SdH experiments are usually performed at high-field facilities like the High Field Magnet Laboratory in Netherlands, Grenoble High Magnetic Field Laboratory in France, the Tsukuba Magnet Laboratory in Japan or the National High Magnetic Field Laboratory in the United States.
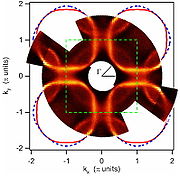 The most direct experimental technique to resolve the electronic structure of crystals in the momentum-energy space (see reciprocal lattice
The most direct experimental technique to resolve the electronic structure of crystals in the momentum-energy space (see reciprocal lattice
), and, consequently, the Fermi surface, is the angle resolved photoemission spectroscopy (ARPES
). An example of the Fermi surface of superconducting cuprates
measured by ARPES
is shown in figure.
With positron annihilation the two photons carry the momentum of the electron away; as the momentum of a thermalized positron is negligible, in this way also information about the momentum distribution can be obtained. Because the positron can be polarized, also the momentum distribution for the two spin
states in magnetized materials can be obtained. Another advantage with de Haas–Van Alphen-effect is that the technique can be applied to non-dilute alloys. In this way the first determination of a smeared Fermi surface in a 30% alloy was obtained in 1978.
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s, semimetals, and doped semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, which allows a maximum of one electron per quantum state.
Theory
Consider a spinless ideal Fermi gasFermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
of
 particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy
particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy  is given by
is given by
where,
 is the mean occupation number
is the mean occupation number
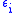 is the energy of the
is the energy of the 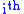 state
state
 is the chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
is the chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
(which at zero temperature is the maximum energy the particle can have i.e. Fermi energyFermi energyThe Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
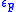 )
)
Suppose we consider the limit
 . Then we have,
. Then we have,
By the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, no two particles can be in the same state. Therefore, in the state of lowest energy, the particles fill up all energy levels till
 , which is equivalent to saying that
, which is equivalent to saying that  is the energy level below which there are exactly
is the energy level below which there are exactly  states.
states.In momentum space, these particles fill up a sphere of radius
 , the surface of which is called the Fermi surface
, the surface of which is called the Fermi surfaceThe linear response of a metal to an electric, magnetic or thermal gradient is determined by the shape of the Fermi surface, because currents are due to changes in the occupancy of states near the Fermi energy. Free-electron Fermi surfaces are spheres of radius
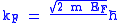 determined by the valence electron concentration where
determined by the valence electron concentration where  is the reduced Planck's constant. A material whose Fermi level falls in a gap between bands is an insulator
is the reduced Planck's constant. A material whose Fermi level falls in a gap between bands is an insulatorElectrical insulation
thumb|250px|[[Coaxial Cable]] with dielectric insulator supporting a central coreThis article refers to electrical insulation. For insulation of heat, see Thermal insulation...
or semiconductor depending on the size of the bandgap. When a material's Fermi level falls in a bandgap, there is no Fermi surface.

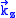 direction. Often in a metal the Fermi surface radius
direction. Often in a metal the Fermi surface radius  is larger than the size of the first Brillouin zone
is larger than the size of the first Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
which results in a portion of the Fermi surface lying in the second (or higher) zones. As with the band structure itself, the Fermi surface can be displayed in an extended-zone scheme where
 is allowed to have arbitrarily large values or a reduced-zone scheme where wavevectors are shown modulo
is allowed to have arbitrarily large values or a reduced-zone scheme where wavevectors are shown moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
 (in the 1-dimensional case) where a is the lattice constant
(in the 1-dimensional case) where a is the lattice constantLattice constant
The lattice constant [or lattice parameter] refers to the constant distance between unit cells in a crystal lattice. Lattices in three dimensions generally have three lattice constants, referred to as a, b, and c. However, in the special case of cubic crystal structures, all of the constants are...
. In the three dimensional case the reduced zone scheme means that from any wavevector
 there is an appropriate number of reciprocal lattice vectors
there is an appropriate number of reciprocal lattice vectors  subtracted that the new
subtracted that the new  now is closer to the origin in
now is closer to the origin in 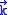 -space than to any
-space than to any  . Solids with a large density of states at the Fermi level become unstable at low temperatures and tend to form ground state
. Solids with a large density of states at the Fermi level become unstable at low temperatures and tend to form ground stateGround state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
s where the condensation energy comes from opening a gap at the Fermi surface. Examples of such ground states are superconductors, ferromagnets, Jahn–Teller distortions and spin density wave
Spin density wave
Spin-density wave and charge-density wave are names for two similar low-energy ordered states of solids. Both these states occur at low temperature in anisotropic, low-dimensional materials or in metals that have high densities of states at the Fermi level N...
s.
The state occupancy of fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s like electrons is governed by Fermi–Dirac statistics so at finite temperatures the Fermi surface is accordingly broadened. In principle all fermion energy level populations are bound by a Fermi surface although the term is not generally used outside of condensed-matter physics.
Experimental determination
Electronic Fermi surfaces have been measured through observation of the oscillation of transport properties in magnetic fields , for example the de Haas-van Alphen effect
, for example the de Haas-van Alphen effectDe Haas-van Alphen effect
The de Haas–van Alphen effect, often abbreviated to dHvA, is a quantum mechanical effect in which the magnetic moment of a pure metal crystal oscillates as the intensity of an applied magnetic field B is increased. Other quantities also oscillate, such as the resistivity , specific heat, and sound...
(dHvA) and the Shubnikov–de Haas effect (SdH). The former is an oscillation in magnetic susceptibility
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
and the latter in resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
. The oscillations are periodic versus
 and occur because of the quantization of energy levels in the plane perpendicular to a magnetic field, a phenomenon first predicted by Lev Landau
and occur because of the quantization of energy levels in the plane perpendicular to a magnetic field, a phenomenon first predicted by Lev LandauLev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
. The new states are called Landau levels and are separated by an energy
 where
where 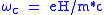 is called the cyclotron frequency
is called the cyclotron frequencyElectron cyclotron resonance
Electron cyclotron resonance is a phenomenon observed both in plasma physics and condensed matter physics. An electron in a static and uniform magnetic field will move in a circle due to the Lorentz force...
,
 is the electronic charge,
is the electronic charge, 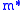 is the electron effective mass and
is the electron effective mass and  is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. In a famous result, Lars Onsager
Lars Onsager
Lars Onsager was a Norwegian-born American physical chemist and theoretical physicist, winner of the 1968 Nobel Prize in Chemistry.He held the Gibbs Professorship of Theoretical Chemistry at Yale University....
proved that the period of oscillation
 is related to the cross-section of the Fermi surface (typically given in
is related to the cross-section of the Fermi surface (typically given in 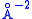 ) perpendicular to the magnetic field direction
) perpendicular to the magnetic field direction 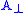 by the equation
by the equation  . Thus the determination of the periods of oscillation for various applied field directions allows mapping of the Fermi surface.
. Thus the determination of the periods of oscillation for various applied field directions allows mapping of the Fermi surface. Observation of the dHvA and SdH oscillations requires magnetic fields large enough that the circumference of the cyclotron orbit is smaller than a mean free path
Mean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
. Therefore dHvA and SdH experiments are usually performed at high-field facilities like the High Field Magnet Laboratory in Netherlands, Grenoble High Magnetic Field Laboratory in France, the Tsukuba Magnet Laboratory in Japan or the National High Magnetic Field Laboratory in the United States.

Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
), and, consequently, the Fermi surface, is the angle resolved photoemission spectroscopy (ARPES
ARPES
Angle-resolved photoemission spectroscopy , also known as ARUPS , is a direct experimental technique to observe the distribution of the electrons in the reciprocal space of solids...
). An example of the Fermi surface of superconducting cuprates
Fermi surface of superconducting cuprates
The electronic structure of superconducting cuprates, also called high temperature superconductors , is highly anisotropic. First, the cuprates are almost two-dimensional : the conducting electrons are mainly localized in the CuO2 layers, the common building blocks of all HTSC compounds...
measured by ARPES
ARPES
Angle-resolved photoemission spectroscopy , also known as ARUPS , is a direct experimental technique to observe the distribution of the electrons in the reciprocal space of solids...
is shown in figure.
With positron annihilation the two photons carry the momentum of the electron away; as the momentum of a thermalized positron is negligible, in this way also information about the momentum distribution can be obtained. Because the positron can be polarized, also the momentum distribution for the two spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
states in magnetized materials can be obtained. Another advantage with de Haas–Van Alphen-effect is that the technique can be applied to non-dilute alloys. In this way the first determination of a smeared Fermi surface in a 30% alloy was obtained in 1978.
See also
- Fermi energyFermi energyThe Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
- Brillouin zoneBrillouin zoneIn mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
- Fermi surface of superconducting cupratesFermi surface of superconducting cupratesThe electronic structure of superconducting cuprates, also called high temperature superconductors , is highly anisotropic. First, the cuprates are almost two-dimensional : the conducting electrons are mainly localized in the CuO2 layers, the common building blocks of all HTSC compounds...
- Kelvin probe force microscopeKelvin probe force microscopeKelvin probe force microscopy , also known as surface potential microscopy, is a noncontact variant of atomic force microscopy that was invented in 1991. With KPFM, the work function of surfaces can be observed at atomic or molecular scales...

