Heavy Fermion
Encyclopedia
In solid-state physics
, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons. Electrons, a kind of fermion
, found in such materials are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free-electron theory. The properties of the heavy fermion compounds derive from the partly filled f-orbitals of rare earth
or actinide
ions which behave like localized magnetic moment
s. The name "heavy fermion" comes from the fact that below a characteristic temperature (typically below 10K) the conduction electrons in these metallic compounds behave as if they had an effective mass
up to 1000 times the free-electron mass. This large effective mass is also reflected a large contribution to the resistivity
from electron-electron scattering via the Kadowaki Woods ratio. The heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
While investigations on doped superconductors led to the conclusion that the existence of localized magnetic moments and superconductivity in one material was incompatible, the opposite was shown, when in 1979 Steglich
et al. discovered heavy fermion superconductivity
in the material CeCu2Si2.
The discovery of a quantum critical point
and non fermi liquid behavior in the phase diagram of heavy fermion compounds by von Löhneysen et al. in 1995 led to a new rise of interest in the research of theses compounds.
Heavy fermion materials play an important role in current scientific research, acting as prototypical materials for unconventional superconductivity, non fermi liquid behavior and quantum critically. The actual interaction between localized magnetic moments and conduction electrons in heavy fermion compounds is still not completely understood and a topic of ongoing investigation.
Several members of the group of heavy fermion materials, become superconducting below a critical Temperature. The superconduction is unconventional
.
At high temperatures heavy fermion compounds behave like normal metals and the electrons can be described as a fermi gas
, in which the electrons are assumed to be non-interacting fermions. In this case the interaction between the f-electrons, which present a local magnetic moment and the conduction electrons is neglected.
The fermi liquid theory
by Landau provides a good model to describe the properties of most heavy fermion materials at low temperatures. In this theory the electrons are described by quasiparticles, which have the same quantum numbers and charge, but the interaction of the electrons is taken into account by introducing an effective mass, which differs from the actual mass of a free electron.
measurements. Therefore the sample is irradiated by electromagnetic waves
with tuneable wavelength
. Measuring the reflected or transmitted light then reveals the characteristic energies of the sample.
Above the characteristic coherence temperature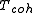
, heavy fermion materials behave like normal metals; i.e their optical response is described by the Drude model
. But compared to a good metal, heavy fermion compounds at high temperatures have a high scattering rate because of the large density of local magnetic moments (at least one f-electron per unit cell), which cause (incoherent) Kondo
scattering. Due to the high scattering rate, the conductivity for dc and at low frequencies is rather low. A conductivity roll-off (Drude roll-off) occurs at the frequency which corresponds to the relaxation rate.
Below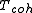
, the localized f-electrons hybridize with the conduction electrons. This leads to the enhanced effective mass and a hybridization gap develops. In contrast to Kondo insulator
s, the chemical potential of heavy fermion compounds lies within the conduction band. These changes lead to two important features in the optical response of heavy fermions.
The frequency-dependent conductivity of heavy-fermion materials can be expressed by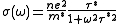
, containing the effective mass 
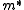and the renormalized relaxation rate 
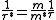. Due to the large effective mass, the renormalized relaxation rate is also enhanced, leading to a narrow Drude roll-off at very low frequencies compared to normal metals.
The gap like feature in the optical conductivity represents directly the hybridization gap, which opens due to the interaction of localized f-electrons and conduction electrons. Since the conductivity does not vanish completely, the observed gap is actually a pseudogap
.
At even higher frequencies we can observe a local maximum in the optical conductivity due to normal interband excitations.
s CP,ph depending cubically on temperature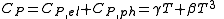
with proportionality constants β and γ.
In the temperature range mentioned above, the electronic contribution is the major part of the specific heat. For the free-electron gas
— a simple model system that neglects electron interaction — or metals that could be described by it, the electronic specific heat is given by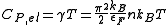
with Boltzmann's factor kB, the electron density n and the Fermi energy
εF (the highest single particle energy of occupied electronic states). The proportionality constant γ is called the Sommerfeld parameter.
(as for the free-electron gas), the Fermi energy
εF is inversely proportional to the particle's mass m: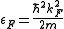
where kF stands for the Fermi wave number that depends on the electron density and is the absolute value of the wave number of the highest occupied electron state. Thus, because the Sommerfeld parameter γ is inversely proportional to εF, γ is proportional to the particle's mass and for high values of γ, the metal behaves as a free electron gas in which the conduction electrons have a high thermal effective mass.
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons. Electrons, a kind of fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
, found in such materials are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free-electron theory. The properties of the heavy fermion compounds derive from the partly filled f-orbitals of rare earth
Rare earth element
As defined by IUPAC, rare earth elements or rare earth metals are a set of seventeen chemical elements in the periodic table, specifically the fifteen lanthanides plus scandium and yttrium...
or actinide
Actinide
The actinide or actinoid series encompasses the 15 metallic chemical elements with atomic numbers from 89 to 103, actinium through lawrencium.The actinide series derives its name from the group 3 element actinium...
ions which behave like localized magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
s. The name "heavy fermion" comes from the fact that below a characteristic temperature (typically below 10K) the conduction electrons in these metallic compounds behave as if they had an effective mass
Effective mass
In solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
up to 1000 times the free-electron mass. This large effective mass is also reflected a large contribution to the resistivity
Resistivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
from electron-electron scattering via the Kadowaki Woods ratio. The heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
Historical Overview
Heavy fermion behavior was discovered by Andres, Graebner and Ott in 1975, who observed enormous magnitudes of the linear specific heat capacity in CeAl3.While investigations on doped superconductors led to the conclusion that the existence of localized magnetic moments and superconductivity in one material was incompatible, the opposite was shown, when in 1979 Steglich
Frank Steglich
Frank Steglich is a German physicist.He received the Gottfried Wilhelm Leibniz Prize by the Deutsche Forschungsgemeinschaft in 1986 and a number of other recognitions...
et al. discovered heavy fermion superconductivity
Heavy fermion superconductor
Heavy fermion superconductors are a type of Unconventional superconductor.The first heavy fermion superconductor, CeCu2Si2, was discovered by Frank Steglich in 1978....
in the material CeCu2Si2.
The discovery of a quantum critical point
Quantum Critical Point
A quantum critical point is a special class of continuous phase transition that takes place at the absolute zero of temperature, typically in a material where the phase transition temperature has been driven to zero by the application of a pressure, field or through doping.Conventional phase...
and non fermi liquid behavior in the phase diagram of heavy fermion compounds by von Löhneysen et al. in 1995 led to a new rise of interest in the research of theses compounds.
Heavy fermion materials play an important role in current scientific research, acting as prototypical materials for unconventional superconductivity, non fermi liquid behavior and quantum critically. The actual interaction between localized magnetic moments and conduction electrons in heavy fermion compounds is still not completely understood and a topic of ongoing investigation.
Properties of heavy fermion materials
Heavy Fermion materials belong to the group of strongly correlated electron systems.Several members of the group of heavy fermion materials, become superconducting below a critical Temperature. The superconduction is unconventional
Unconventional superconductor
Unconventional superconductors are materials that display superconductivity which does not conform to either the conventional BCS theory or the Nikolay Bogolyubov's theory or its extensions....
.
At high temperatures heavy fermion compounds behave like normal metals and the electrons can be described as a fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
, in which the electrons are assumed to be non-interacting fermions. In this case the interaction between the f-electrons, which present a local magnetic moment and the conduction electrons is neglected.
The fermi liquid theory
Fermi liquid
Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interaction between the particles of the many-body system does not need to be small...
by Landau provides a good model to describe the properties of most heavy fermion materials at low temperatures. In this theory the electrons are described by quasiparticles, which have the same quantum numbers and charge, but the interaction of the electrons is taken into account by introducing an effective mass, which differs from the actual mass of a free electron.
Optical Properties
In order to obtain the optical properties of heavy fermion systems, these materials have been investigated by optical spectroscopySpectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
measurements. Therefore the sample is irradiated by electromagnetic waves
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
with tuneable wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
. Measuring the reflected or transmitted light then reveals the characteristic energies of the sample.
Above the characteristic coherence temperature
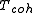, heavy fermion materials behave like normal metals; i.e their optical response is described by the Drude modelDrude model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...
. But compared to a good metal, heavy fermion compounds at high temperatures have a high scattering rate because of the large density of local magnetic moments (at least one f-electron per unit cell), which cause (incoherent) Kondo
Kondo effect
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities. It is a measure of how electrical resistivity changes with temperature....
scattering. Due to the high scattering rate, the conductivity for dc and at low frequencies is rather low. A conductivity roll-off (Drude roll-off) occurs at the frequency which corresponds to the relaxation rate.
Below
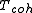, the localized f-electrons hybridize with the conduction electrons. This leads to the enhanced effective mass and a hybridization gap develops. In contrast to Kondo insulatorKondo insulator
In solid-state physics, Kondo insulators are understood as materials with strongly correlated electrons, that open up a narrow band gap at low temperatures with the chemical potential lying in the gap, whereas in heavy fermions the chemical potential is located in the...
s, the chemical potential of heavy fermion compounds lies within the conduction band. These changes lead to two important features in the optical response of heavy fermions.
The frequency-dependent conductivity of heavy-fermion materials can be expressed by
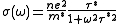, containing the effective mass 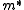and the renormalized relaxation rate 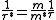. Due to the large effective mass, the renormalized relaxation rate is also enhanced, leading to a narrow Drude roll-off at very low frequencies compared to normal metals.The gap like feature in the optical conductivity represents directly the hybridization gap, which opens due to the interaction of localized f-electrons and conduction electrons. Since the conductivity does not vanish completely, the observed gap is actually a pseudogap
Pseudogap
The term 'pseudogap' was coined by Nevill Mott in 1968 to indicate a minimum in the density of states at the Fermi energy, N, resulting from Coulomb repulsion between electrons in the same atom, a bandgap in a disordered material or a combination of these...
.
At even higher frequencies we can observe a local maximum in the optical conductivity due to normal interband excitations.
The specific heat for normal metals
At low temperature and for normal metals, the specific heat CP consists of the specific heat of the electrons CP,el depending linearly on temperature T and of the specific heat of the crystal lattice vibrations or the phononPhonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s CP,ph depending cubically on temperature
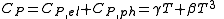
with proportionality constants β and γ.
In the temperature range mentioned above, the electronic contribution is the major part of the specific heat. For the free-electron gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
— a simple model system that neglects electron interaction — or metals that could be described by it, the electronic specific heat is given by
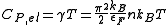
with Boltzmann's factor kB, the electron density n and the Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
εF (the highest single particle energy of occupied electronic states). The proportionality constant γ is called the Sommerfeld parameter.
Relation between heat capacity and "thermal effective mass"
For electrons with a quadratic dispersion relationDispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
(as for the free-electron gas), the Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
εF is inversely proportional to the particle's mass m:
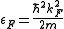
where kF stands for the Fermi wave number that depends on the electron density and is the absolute value of the wave number of the highest occupied electron state. Thus, because the Sommerfeld parameter γ is inversely proportional to εF, γ is proportional to the particle's mass and for high values of γ, the metal behaves as a free electron gas in which the conduction electrons have a high thermal effective mass.
Example: heat capacity for UBe13 at low temperatures
Experimental results for the specific heat of the heavy fermion compound UBe13 show a peak at a temperature around 0.75 K that goes down to zero with a high slope if the temperature approaches 0 K. Due to this peak, the γ-factor is much higher than for the free-electron gas in this temperature range. In contrast, above 6 K the specific heat for this heavy fermion compound approaches the value expected from free-electron theory.Books
- Kittel, CharlesCharles KittelCharles Kittel is an American physicist. He was a Professor at University of California, Berkeley from 1951 and has been Professor Emeritus since 1978.- Life and work :...
(1996) Introduction to Solid State Physics, 7th Ed., John Wiley and Sons, Inc. - Marder, M.P. (2000), Condensed Matter Physics, John Wiley & Sons, New York.
- Hewson, A.C. (1993), The Kondo Problem to Heavy Fermions, Cambridge University Press.
- Fulde, P. (1995), Electron Correlations in Molecules and Solids, Springer, Berlin.