
Sylvester's criterion
Encyclopedia
In mathematics, Sylvester’s criterion is a necessary and sufficient criterion to determine whether a Hermitian matrix is positive-definite
. It is named after James Joseph Sylvester
.
Sylvester's criterion states that a Hermitian matrix M is positive-definite if and only if all the following matrices have a positive determinant
:
In other words, all of the leading principal minors must be positive.
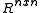 , therefore only for nonsingular real-symmetric matrices
, therefore only for nonsingular real-symmetric matrices
Positive Definite or Semidefinite Matrix: A symmetric matrix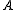 whose eigenvalues are positive (λ>0) is called positive definite
whose eigenvalues are positive (λ>0) is called positive definite
, and when the eigenvalues are just nonnegative (λ≥0),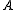 is said to be positive semidefinite.
is said to be positive semidefinite.
Theorem I: A real-symmetric matrix has nonnegative eigenvalues if and only if
has nonnegative eigenvalues if and only if 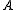 can be factored as
can be factored as 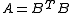 , and all eigenvalues are positive if and only if
, and all eigenvalues are positive if and only if 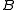 is nonsingular.
is nonsingular.
{| cellspacing="0" cellpadding="1"
|-
|valign="top"| Proof: ||
Necessity:
If A ∈ Rnxn is symmetric, then, by the Spectral theorem
, there is an orthogonal matrix P such that A = PDPT , where D = diag (λ1, λ2, . . . , λn) is real diagonal matrix with entries - eigenvalues of A and P is such that it columns are the eigenvectors of A. If λi ≥ 0 for each i, then D1/2 exists, so A = PDPT = PD1/2D1/2PT = BTB for B = D1/2PT, and λi > 0 for each i if and only if B is nonsingular.
Sufficiency:
Conversely, if A can be factored as A = BTB, then all eigenvalues of A are nonnegative because for any eigenpair (λ, x):
λ=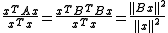 ≥0.
≥0.
|}
Theorem II (The Cholesky decomposition): The symmetric matrix A possesses positive pivots if and only if A can be uniquely factored as A = RTR, where R is an upper-triangular matrix with positive diagonal entries. This is known as the Cholesky decomposition
of A, and R is called the Cholesky factor of A.
{| cellspacing="0" cellpadding="1"
|-
|valign="top"| Proof: ||
Necessity: If A possesses positive pivots (therefore A possesses an LU factorization: A=L.U' ), then, it has an LDU factorization A = LDU=LDLT in which D = diag (u11, u22, . . . , unn) is the diagonal matrix containing the pivots uii > 0.
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. It is named after James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
.
Sylvester's criterion states that a Hermitian matrix M is positive-definite if and only if all the following matrices have a positive determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
:
- the upper left 1-by-1 corner of
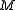 ,
, - the upper left 2-by-2 corner of
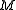 ,
, - the upper left 3-by-3 corner of
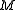 ,
, - ...
-
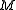 itself.
itself.
In other words, all of the leading principal minors must be positive.
Proof
The proof is only for nonsingular Hermitian matrix with coefficients in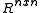 , therefore only for nonsingular real-symmetric matrices
, therefore only for nonsingular real-symmetric matricesPositive Definite or Semidefinite Matrix: A symmetric matrix
 whose eigenvalues are positive (λ>0) is called positive definite
whose eigenvalues are positive (λ>0) is called positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, and when the eigenvalues are just nonnegative (λ≥0),
 is said to be positive semidefinite.
is said to be positive semidefinite.Theorem I: A real-symmetric matrix
 has nonnegative eigenvalues if and only if
has nonnegative eigenvalues if and only if  can be factored as
can be factored as 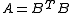 , and all eigenvalues are positive if and only if
, and all eigenvalues are positive if and only if 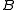 is nonsingular.
is nonsingular.{| cellspacing="0" cellpadding="1"
|-
|valign="top"| Proof: ||
Necessity:
If A ∈ Rnxn is symmetric, then, by the Spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, there is an orthogonal matrix P such that A = PDPT , where D = diag (λ1, λ2, . . . , λn) is real diagonal matrix with entries - eigenvalues of A and P is such that it columns are the eigenvectors of A. If λi ≥ 0 for each i, then D1/2 exists, so A = PDPT = PD1/2D1/2PT = BTB for B = D1/2PT, and λi > 0 for each i if and only if B is nonsingular.
Sufficiency:
Conversely, if A can be factored as A = BTB, then all eigenvalues of A are nonnegative because for any eigenpair (λ, x):
λ=
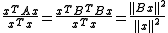 ≥0.
≥0.|}
Theorem II (The Cholesky decomposition): The symmetric matrix A possesses positive pivots if and only if A can be uniquely factored as A = RTR, where R is an upper-triangular matrix with positive diagonal entries. This is known as the Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
of A, and R is called the Cholesky factor of A.
{| cellspacing="0" cellpadding="1"
|-
|valign="top"| Proof: ||
Necessity: If A possesses positive pivots (therefore A possesses an LU factorization: A=L.U' ), then, it has an LDU factorization A = LDU=LDLT in which D = diag (u11, u22, . . . , unn) is the diagonal matrix containing the pivots uii > 0.
-
 x
x 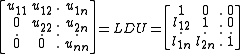 x
x 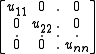 x
x 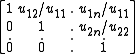
By a uniqueness property of the LDU decomposition, the symmetry of A yields: U=LT, consequently A=LDU=LDLT. Setting R = D1/2LT where D1/2 = diag(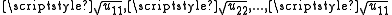 ) yields the desired factorization, because A = LD1/2D1/2LT = RTR, and R is upper triangular with positive diagonal entries.
) yields the desired factorization, because A = LD1/2D1/2LT = RTR, and R is upper triangular with positive diagonal entries.
Sufficiency: Conversely, if A = RRT , where R is lower triangular with a positive diagonal, then factoring the diagonal entries out of R is as follows:-
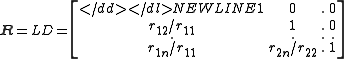 x
x 
R = LD, where L is lower triangular with a unit diagonal and D is the diagonal matrix whose diagonal entries are the rii ’s. Consequently, A = LD2LT is the LDU factorization for A, and thus the pivots must be positive because they are the diagonal entries in D2.
|}
Theorem III: Let Ak be the k × k leading principal submatrix of An×n. If A has an LU factorization A = LU, then det(Ak) = u11u22 · · · ukk, and the k-th pivot is ukk =det(A1) = a11 for k = 1, ukk=det(Ak)/det(Ak−1) for k = 2, 3, . . . , n.
Combining Theorem II with Theorem III yields:
Statement I: If the symmetric matrix A can be factored as A=RTR where R is an upper-triangular matrix with positive diagonal entries, then all the pivots of A are positive (by Theorem II), therefore all the leading principal minors of A are positive (by Theorem III).
Statement II: If the nonsingular symmetric matrix A can be factored as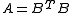 , then the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
, then the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
(closely related to Gram-Schmidt process) of B (B=QR) yields: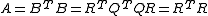 , where Q is orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, where Q is orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and R is upper triangular matrixTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
.
Namely Statement II requires the non-singularity of the symmetric matrix A.
Combining Theorem I with Statement I and Statement II yields:
Statement III: If the real-symmetric matrix A is positive definite then A possess factorization of the form A=BTB, where B is nonsingular (Theorem I), the expression A=BTB implies that A possess factorization of the form A=RTR where R is an upper-triangular matrix with positive diagonal entries (Statement II), therefore all the leading principal minors of A are positive (Statement I).
In other words, Statement III states:
Sylvester's Criterion: The real-symmetric matrix A is positive definite if and only if all the leading principal minors of A are positive.
The sufficiency and necessity conditions automatically holds because they were proven for each of the above theorems.
-

