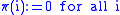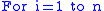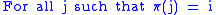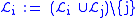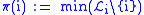Symbolic Cholesky decomposition
Encyclopedia
In the mathematical
subfield of numerical analysis
the symbolic Cholesky decomposition is an algorithm
used to determine the non-zero pattern for the
factors of a symmetric sparse matrix
when applying the Cholesky decomposition
or variants.
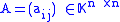
be a sparse symmetric positive definite matrix with elements from a field
, which we wish to factorize as
.
In order to implement an efficient sparse factorization it has been found to be necessary to determine the non zero structure of the factors before doing any numerical work. To write the algorithm down we use the following notation:
The following algorithm gives an efficient
symbolic factorization of
:
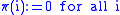
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subfield of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
the symbolic Cholesky decomposition is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used to determine the non-zero pattern for the
factors of a symmetric sparse matrixSparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
when applying the Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
or variants.
Algorithm
Let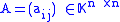be a sparse symmetric positive definite matrix with elements from a field
, which we wish to factorize as.In order to implement an efficient sparse factorization it has been found to be necessary to determine the non zero structure of the factors before doing any numerical work. To write the algorithm down we use the following notation:
- Let
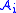and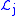 
be sets representing the non-zero patterns of columns i and j (below the diagonal only, and including diagonal elements) of matrices 
and 
respectively. - Take
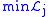to mean the smallest element of 
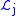. - Use a parent function
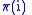to define the elimination tree within the matrix.
The following algorithm gives an efficient
symbolic factorization of
:
