Synergetics coordinates
Encyclopedia
Synergetics coordinates is Clifford Nelson's attempt to describe, from another mathematical point of view, Buckminster Fuller
's '60 degree coordinate system' for understanding nature. Synergetics
is the word Fuller used to label his approach to mathematics
.
of synergetics coordinates uses only one type of simplex
(triangle
, tetrahedron
, pentachoron
, ..., n-simplex) as space
units, and in fact uses a regular
simplex, rather like Cartesian coordinates use hypercubes (square
, cube
, tesseract
, ..., n-cube.)
 The n Synergetics coordinates axes are perpendicular to the n defining geometric objects that define a regular simplex; 2 end points for line segments, 3 lines for triangles, 4 planes for tetrahedrons etc.. The angles between the directions of the coordinate axes are Arc Cosine (-1/(n-1)). The coordinates can be positive or negative or zero and so can their sum. The sum of the n coordinates is the edge length of the regular simplex defined by moving the n geometric objects in increments of the height of the n-1 dimensional regular simplex that has an edge length of one. If the sum of the n coordinates is negative the triangle (n = 3) or tetrahedron (n = 4) is upside down and inside out.
The n Synergetics coordinates axes are perpendicular to the n defining geometric objects that define a regular simplex; 2 end points for line segments, 3 lines for triangles, 4 planes for tetrahedrons etc.. The angles between the directions of the coordinate axes are Arc Cosine (-1/(n-1)). The coordinates can be positive or negative or zero and so can their sum. The sum of the n coordinates is the edge length of the regular simplex defined by moving the n geometric objects in increments of the height of the n-1 dimensional regular simplex that has an edge length of one. If the sum of the n coordinates is negative the triangle (n = 3) or tetrahedron (n = 4) is upside down and inside out.
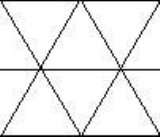
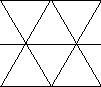
are in a grid
of equilateral
triangles and are of the form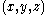 such that
such that 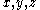 are equal to or greater than 0.
are equal to or greater than 0.
Regular tetrahedral coordinates are in a Euclidean 3-space
'grid' of equilateral tetrahedra and are of the form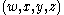 such that
such that  are equal to or greater than 0.
are equal to or greater than 0.
Buckminster Fuller
Richard Buckminster “Bucky” Fuller was an American systems theorist, author, designer, inventor, futurist and second president of Mensa International, the high IQ society....
's '60 degree coordinate system' for understanding nature. Synergetics
Synergetics (Fuller)
Synergetics is the empirical study of systems in transformation, with an emphasis on total system behavior unpredicted by the behavior of any isolated components, including humanity’s role as both participant and observer....
is the word Fuller used to label his approach to mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
.
Geometric definition
A systemTheory of Forms
Plato's theory of Forms or theory of Ideas asserts that non-material abstract forms , and not the material world of change known to us through sensation, possess the highest and most fundamental kind of reality. When used in this sense, the word form is often capitalized...
of synergetics coordinates uses only one type of simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
, tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, pentachoron
Pentachoron
In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid...
, ..., n-simplex) as space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
units, and in fact uses a regular
Regular
The term regular can mean normal or obeying rules. Regular may refer to:In organizations:* Regular Army for military usage* Regular clergy, members of a religious order subject to a rule of life* Regular Force for usage in the Canadian Forces...
simplex, rather like Cartesian coordinates use hypercubes (square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
, ..., n-cube.)

Algebraic examples
Regular triangular coordinatesTriangular coordinates
The term triangular coordinates may refer to any of at least three related systems of coordinates in the Euclidean plane:* a special case of barycentric coordinates for a triangle, in which case it is known as a ternary plot or areal coordinates, among other names,* trilinear coordinates, in which...
are in a grid
Lattice graph
The terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
of equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
triangles and are of the form
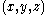 such that
such that 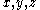 are equal to or greater than 0.
are equal to or greater than 0.Regular tetrahedral coordinates are in a Euclidean 3-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
'grid' of equilateral tetrahedra and are of the form
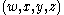 such that
such that  are equal to or greater than 0.
are equal to or greater than 0.See also
- Barycentric coordinates (mathematics)Barycentric coordinates (mathematics)In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
- Trilinear coordinatesTrilinear coordinatesIn geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
- Quadray coordinatesQuadray coordinatesQuadray coordinates, also known as tetray coordinates or Chakovian coordinates, were developed by David Chako, Tom Ace, Kirby Urner, Darrel Jarmusch et al., as another take on simplicial coordinates, a coordinate system using the simplex or tetrahedron as its basis polyhedron.-Geometric...
External links
- Clifford J. Nelson. Synergetics Coordinates

