Synthetic division
Encyclopedia
Synthetic division is a method of performing polynomial long division
, with less writing and fewer calculations. It is mostly taught for division by binomials of the form
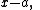
but the method generalizes to division by any monic polynomial. This method can be used instead of long division
on integers by considering 10 = x and only substituting 10 back in at the end.
The most useful aspects of synthetic division are that it allows one to calculate without writing variables and uses fewer calculations. As well, it takes significantly less space than long division. Most importantly, the subtractions in long division are converted to additions by switching the signs at the very beginning, preventing sign errors.
Synthetic division for linear denominators is also called division through Ruffini's rule
.
.
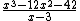
Write the coefficients of the polynomial to be divided at the top (the zero is for the unseen 0x).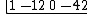
Negate the coefficients of the divisor.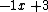
Write in every coefficient of the divisor but the first one on the left.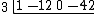
Note the change of sign from −3 to 3. "Drop" the first coefficient after the bar to the last row.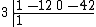
Multiply the dropped number by the number before the bar, and place it in the next column.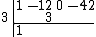
Perform an addition in the next column.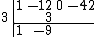
Repeat the previous two steps and the following is obtained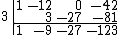
Count the terms to the left of the bar. Since there is only one, the remainder has degree one. Mark the separation with a vertical bar.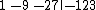
The terms are written with increasing degree from right to left beginning with degree zero for both the remainder and the result.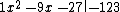
The result of our division is: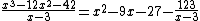
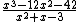
We concern ourselves only with the coefficients.
Write the coefficients of the polynomial to be divided at the top.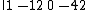
Negate the coefficients of the divisor.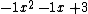
Write in every coefficient but the first one on the left in an upward right diagonal (see next diagram).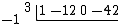
Note the change of sign from 1 to −1 and from −3 to 3 . "Drop" the first coefficient after the bar to the last row.
Multiply the dropped number by the diagonal before the bar, and place the resulting entries diagonally to the right from the dropped entry.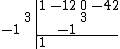
Perform an addition in the next column.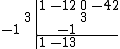
Repeat the previous two steps until you would go past the entries at the top with the next diagonal.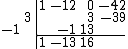
Then simply add up any remaining columns.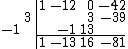
Count the terms to the left of the bar. Since there are two, the remainder has degree one. Mark the separation with a vertical bar.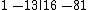
The terms are written with increasing degree from right to left beginning with degree zero for both the remainder and the result.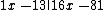
The result of our division is: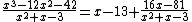
However, the diagonal format above becomes less space-efficient when the degree of the divisor exceeds half of the degree of the dividend. It is easy to see that we have complete freedom to write each product in any row, as long as it is in the correct column. So the algorithm can be compactified by a greedy strategy, as illustrated in the division below.
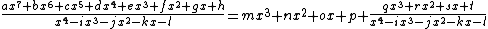
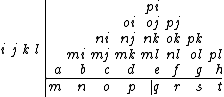
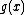with its leading co-efficient (call it a)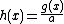
then using synthetic division with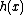
as the divisor, and then multiplying the quotient by a to get the quotient of the original division (the remainder stays the same). But this often produces unsightly fractions which get removed later, and is thus more prone to error. It is possible to do it without first dividing the co-efficients of 
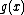by a.
As can be observed by first performing long division with such a non-monic divisor, the co-efficients of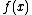
are divided by the leading co-efficient of 
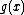after "dropping", and before multiplying.
Let's illustrate by performing the following division:
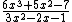
A slightly modified table is used:
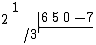
Note the extra row at the bottom. This is used to write values found by dividing the "dropped" values by the leading co-efficient of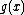
(in this case, indicated by the /3; note that, unlike the rest of the co-efficients of 
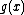, the sign of this number is not changed).
Next, the first co-efficient of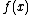
is dropped as usual:
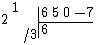
and then the dropped value is divided by 3 and placed in the row below:
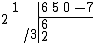
Next, the new (divided) value is used to fill the top rows with multiples of 2 and 1, as in the expanded technique:
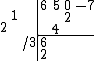
The 5 is dropped next, with the obligatory adding of the 4 below it, and the answer is divided again:
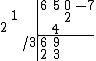
Then the 3 is used to fill the top rows:
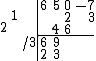
At this point, if, after getting the third sum, we were to try and use it to fill the top rows, we would "fall off" the right side, thus the third value is the first co-efficient of the remainder, as in regular synthetic division. But the values of the remainder are not divided by the leading co-efficient of the divisor:
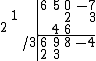
Now we can read of the co-efficients of the answer. As in expanded synthetic division, the last two values (2 is one less than the degree of the divisor) are the co-efficients of the remainder, and the remaining values are the co-efficients of the quotient:
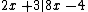
and the result is
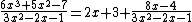
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
, with less writing and fewer calculations. It is mostly taught for division by binomials of the form
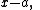
but the method generalizes to division by any monic polynomial. This method can be used instead of long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
on integers by considering 10 = x and only substituting 10 back in at the end.
The most useful aspects of synthetic division are that it allows one to calculate without writing variables and uses fewer calculations. As well, it takes significantly less space than long division. Most importantly, the subtractions in long division are converted to additions by switching the signs at the very beginning, preventing sign errors.
Synthetic division for linear denominators is also called division through Ruffini's rule
Ruffini's rule
In mathematics, Ruffini's rule allows the rapid division of any polynomial by a binomial of the form x − r. It was described by Paolo Ruffini in 1809. Ruffini's rule is a special case of synthetic division when the divisor is a linear factor. The Horner scheme is a fast algorithm for dividing...
.
Regular synthetic division
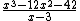
The first example is synthetic division with only a monic linear denominator .Write the coefficients of the polynomial to be divided at the top (the zero is for the unseen 0x).
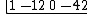
Negate the coefficients of the divisor.
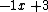
Write in every coefficient of the divisor but the first one on the left.
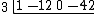
Note the change of sign from −3 to 3. "Drop" the first coefficient after the bar to the last row.
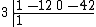
Multiply the dropped number by the number before the bar, and place it in the next column.
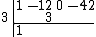
Perform an addition in the next column.
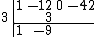
Repeat the previous two steps and the following is obtained
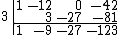
Count the terms to the left of the bar. Since there is only one, the remainder has degree one. Mark the separation with a vertical bar.
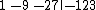
The terms are written with increasing degree from right to left beginning with degree zero for both the remainder and the result.
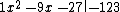
The result of our division is:
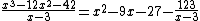
Expanded synthetic division
This method works for bigger divisors with only a slight modification with changes in bold. Using the same steps as before, let's try to perform the following division: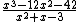We concern ourselves only with the coefficients.
Write the coefficients of the polynomial to be divided at the top.
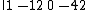
Negate the coefficients of the divisor.
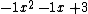
Write in every coefficient but the first one on the left in an upward right diagonal (see next diagram).
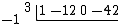
Note the change of sign from 1 to −1 and from −3 to 3 . "Drop" the first coefficient after the bar to the last row.
Multiply the dropped number by the diagonal before the bar, and place the resulting entries diagonally to the right from the dropped entry.
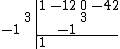
Perform an addition in the next column.
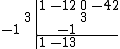
Repeat the previous two steps until you would go past the entries at the top with the next diagonal.
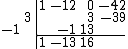
Then simply add up any remaining columns.
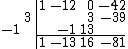
Count the terms to the left of the bar. Since there are two, the remainder has degree one. Mark the separation with a vertical bar.
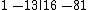
The terms are written with increasing degree from right to left beginning with degree zero for both the remainder and the result.
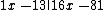
The result of our division is:
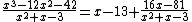
However, the diagonal format above becomes less space-efficient when the degree of the divisor exceeds half of the degree of the dividend. It is easy to see that we have complete freedom to write each product in any row, as long as it is in the correct column. So the algorithm can be compactified by a greedy strategy, as illustrated in the division below.
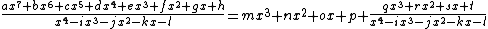
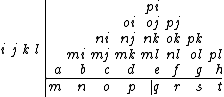
For non-monic divisors
With a little prodding, the expanded technique may be generalised even further to work for any polynomial, not just monics. The usual way of doing this would be to divide the divisor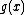 with its leading co-efficient (call it a)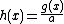then using synthetic division with
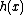as the divisor, and then multiplying the quotient by a to get the quotient of the original division (the remainder stays the same). But this often produces unsightly fractions which get removed later, and is thus more prone to error. It is possible to do it without first dividing the co-efficients of 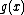by a.As can be observed by first performing long division with such a non-monic divisor, the co-efficients of
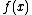are divided by the leading co-efficient of 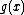after "dropping", and before multiplying.Let's illustrate by performing the following division:
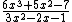
A slightly modified table is used:
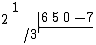
Note the extra row at the bottom. This is used to write values found by dividing the "dropped" values by the leading co-efficient of
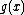(in this case, indicated by the /3; note that, unlike the rest of the co-efficients of , the sign of this number is not changed).Next, the first co-efficient of
is dropped as usual: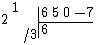and then the dropped value is divided by 3 and placed in the row below:
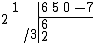
Next, the new (divided) value is used to fill the top rows with multiples of 2 and 1, as in the expanded technique:
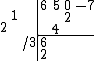
The 5 is dropped next, with the obligatory adding of the 4 below it, and the answer is divided again:
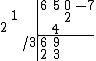
Then the 3 is used to fill the top rows:
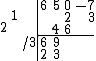
At this point, if, after getting the third sum, we were to try and use it to fill the top rows, we would "fall off" the right side, thus the third value is the first co-efficient of the remainder, as in regular synthetic division. But the values of the remainder are not divided by the leading co-efficient of the divisor:
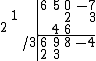
Now we can read of the co-efficients of the answer. As in expanded synthetic division, the last two values (2 is one less than the degree of the divisor) are the co-efficients of the remainder, and the remaining values are the co-efficients of the quotient:
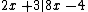
and the result is
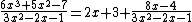
See also
- Polynomial remainder theoremPolynomial remainder theoremIn algebra, the polynomial remainder theorem or little Bézout's theorem is an application of polynomial long division. It states that the remainder of a polynomial f\, divided by a linear divisor x-a\, is equal to f \,.- Example :...
- Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
- Gröbner basisGröbner basisIn computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
- Greatest common divisor of two polynomialsGreatest common divisor of two polynomialsInformally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
- Horner schemeHorner schemeIn numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...