Szpilrajn Extension Theorem
Encyclopedia
In mathematics, the Szpilrajn extension theorem, due to (later called Edward Marczewski
), is one of many examples of the use of the axiom of choice (in the form of Zorn's lemma
) to find a maximal of a set with certain given properties.
The theorem states that, given a binary relation
R that is irreflexive and transitive
it is always possible to find an extension of the relation (i.e. a relation T that strictly includes R) which is asymmetric
, negatively transitive and connected
.
First of all, we need some definitions to be clear upon the terminology we will use speaking about relations with particular properties.
on a generic set 
, we say that 
is negatively transitive if
Note that negative transitivity can also be rewritten as :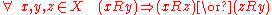
, simply using the fact that 
can be rewritten as 
on a generic set 
, we say that R is connected (weakly) if :
either 
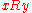or 
.
To enounce precisely the theorem, we need yet a couple of definitions and a useful, simple lemma.
such that 
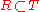and T is another strict partial order on X.
This lemma can be easily proved, by taking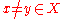
such that 
, which exists since the relation is not connected.
we can define another relation:
Finally, set
which is trivially an extension of R and another strict partial order on X.
We want to show the existence of a maximal element in
with respect to set inclusion.
To do this, we will use Zorn's Lemma. First of all we want to verify the hypothesis of the Lemma, hence that any chain (respect to inclusion) of
admits an upper bound
in
.
Let
be a chain in 
.
Define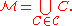
Clearly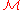
is an upper bound to the chain, but we have to show that 
, hence that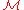 
is another strict partial order which extends R.
Obviously it contains R, as all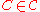
contains R, and it is irreflexive, as
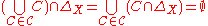, since any
is irreflexive,
We have to show that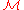
is transitive and here we use the chain properties of 
.
Let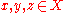
such that 
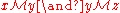iff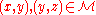 
.
As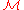
is defined as a union of sets, there exists
such that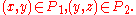 
.
But
is a chain with respect to inclusion, hence it holds that 
or viceversa, so that the two couples of elements of X both belong to the same set in the union, and that set is a transitive relation; then also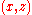
is in that set, hence in 
.
Applying Zorn's Lemma, we deduce that
admits an upper bound with respect to set inclusion; let's call T that bound.
T has to be a complete relation, as if it was not, we could construct (exactly as in the preceding Lemma) another binary relation which strictly extends (strictly includes) T and is a strict partial order, so yet another element of
, contradicting that T is a maximal of 
.
So T is an irreflexive, transitive and complete binary relation on X. But as we observed above, irreflexivity and transitivity give asymmetry that, with transitivity and completeness, give negative transitivity.
Hence T is a strict order on X that extends the partial order R.
Edward Marczewski
Edward Marczewski was a Polish mathematician. His surname until 1940 was Szpilrajn.Marczewski was a member of the Warsaw School of Mathematics...
), is one of many examples of the use of the axiom of choice (in the form of Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
) to find a maximal of a set with certain given properties.
The theorem states that, given a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R that is irreflexive and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
it is always possible to find an extension of the relation (i.e. a relation T that strictly includes R) which is asymmetric
Asymmetric
Something which is asymmetric displays asymmetry. Specific uses of the term may include:*Asymmetric relation for information on such relations in mathematics and set theory*Asymmetric warfare for information and theories of modern war...
, negatively transitive and connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
.
First of all, we need some definitions to be clear upon the terminology we will use speaking about relations with particular properties.
Definition (negative transitivity)
Given a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on a generic set , we say that is negatively transitive if
- where by
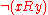we mean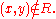 
Note that negative transitivity can also be rewritten as :
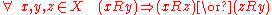, simply using the fact that can be rewritten as Definition (connection)
Given a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
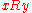on a generic set , we say that R is connected (weakly) if : either or .
- We say that R is strictly connected or complete if
.
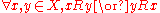Properties
This properties on binary relations can be easily checked by definition:- R is irreflexive and transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
R is asymmetricAsymmetric relationAsymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
. - R is asymmetric, transitive and connected
R is negatively transitive.
To enounce precisely the theorem, we need yet a couple of definitions and a useful, simple lemma.
Definition (strict orders)
- We say that a binary relation R is a strict partial order if it is irreflexive and transitive.
- We say that a binary relation R is a strict order if it is asymmetric, negatively transitive and complete.
Lemma
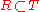Let R be a strict partial order on X. Then there exists another binary relation T on X which is still a strict partial order and extends R, hence: such that and T is another strict partial order on X.This lemma can be easily proved, by taking
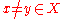such that , which exists since the relation is not connected.- Naming:
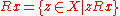
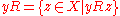
we can define another relation:
Finally, set
which is trivially an extension of R and another strict partial order on X.
Theorem (Szpilrajn's extension theorem)
Let R be a strict partial order on a set X. Then there exists a relation T that extends R and is a strict order on X.Proof
- Let
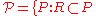, P is a strict partial order on X
.
We want to show the existence of a maximal element in
with respect to set inclusion.To do this, we will use Zorn's Lemma. First of all we want to verify the hypothesis of the Lemma, hence that any chain (respect to inclusion) of
admits an upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
in
.Let
be a chain in .Define
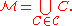
Clearly
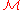is an upper bound to the chain, but we have to show that , hence that 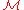is another strict partial order which extends R.Obviously it contains R, as all
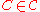contains R, and it is irreflexive, as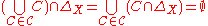, since any is irreflexive,We have to show that
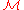is transitive and here we use the chain properties of .Let
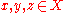such that 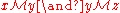iff 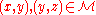.As
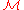is defined as a union of sets, there exists such that 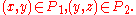.But
is a chain with respect to inclusion, hence it holds that or viceversa, so that the two couples of elements of X both belong to the same set in the union, and that set is a transitive relation; then also
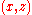is in that set, hence in .Applying Zorn's Lemma, we deduce that
admits an upper bound with respect to set inclusion; let's call T that bound.T has to be a complete relation, as if it was not, we could construct (exactly as in the preceding Lemma) another binary relation which strictly extends (strictly includes) T and is a strict partial order, so yet another element of
, contradicting that T is a maximal of .So T is an irreflexive, transitive and complete binary relation on X. But as we observed above, irreflexivity and transitivity give asymmetry that, with transitivity and completeness, give negative transitivity.
Hence T is a strict order on X that extends the partial order R.