
T-criterion
Encyclopedia
The T-failure criterion is a set of failure criteria
, that can be used to predict both brittle
and ductile failure. These criteria were designed as a replacement for the von Mises yield criterion which predicts the unphysical result that pure hydrostatic tensile loading of metals never leads to failure. The T-criteria use the volumetric stress in addition to the deviatoric stress used by the von Mises criterion and are similar to the Drucker Prager yield criterion
. T-criteria have been designed on the basis of energy considerations and the observation that the reversible elastic
energy density
storage process has a limit which can be used to determine when a material has failed.
The strain energy density stored in the material and calculated by the area under the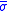 -
-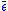 curve represents the total amount of energy stored in the material only in the case of pure shear. In all other cases, there is a divergence between the actual and calculated stored energy in the material, which is maximum in the case of pure hydrostatic loading, where, according to the von Mises criterion, no energy is stored. This paradox is resolved if a second constitutive equation is introduced, that relates hydrostatic pressure p with the volume change
curve represents the total amount of energy stored in the material only in the case of pure shear. In all other cases, there is a divergence between the actual and calculated stored energy in the material, which is maximum in the case of pure hydrostatic loading, where, according to the von Mises criterion, no energy is stored. This paradox is resolved if a second constitutive equation is introduced, that relates hydrostatic pressure p with the volume change  . These two curves, namely
. These two curves, namely  and (p-
and (p- ) are essential for a complete description of material behaviour up to failure. Thus, two criteria must be accounted for when considering failure and two constitutive equations that describe material response. According to this criterion, an upper limit to allowable strains is set either by a critical value ΤV,0 of the elastic energy density due to volume change (dilatational energy) or by a critical value ΤD,0 of the elastic energy density due to change in shape (distortional energy). The volume of material is considered to have failed by extensive plastic flow when the distortional energy Τd reaches the critical value ΤD,0 or by extensive dilatation when the dilatational energy Τv reaches a critical value ΤV,0. The two critical values ΤD,0 and ΤV,0 are considered material constants independent of the shape of the volume of material considered and the induced loading, but dependent on the strain rate and temperature.
) are essential for a complete description of material behaviour up to failure. Thus, two criteria must be accounted for when considering failure and two constitutive equations that describe material response. According to this criterion, an upper limit to allowable strains is set either by a critical value ΤV,0 of the elastic energy density due to volume change (dilatational energy) or by a critical value ΤD,0 of the elastic energy density due to change in shape (distortional energy). The volume of material is considered to have failed by extensive plastic flow when the distortional energy Τd reaches the critical value ΤD,0 or by extensive dilatation when the dilatational energy Τv reaches a critical value ΤV,0. The two critical values ΤD,0 and ΤV,0 are considered material constants independent of the shape of the volume of material considered and the induced loading, but dependent on the strain rate and temperature.
(a) The total increment of a strain component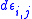 is decomposed into the elastic and the plastic
is decomposed into the elastic and the plastic  increment and
increment and  respectively:
respectively:
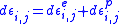 (1)
(1)
(b) The elastic strain increment is given by Hooke’s law:
is given by Hooke’s law:
 (2)
(2)
where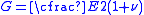 the shear modulus,
the shear modulus,  the Poisson’s ratio and
the Poisson’s ratio and 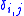 the Krönecker delta.
the Krönecker delta.
(c) The plastic strain increment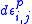 is proportional to the respective deviatoric stress:
is proportional to the respective deviatoric stress:
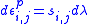 (3)
(3)
where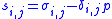 and
and  an infinitesimal scalar. (3) implies that the plastic strain increment:
an infinitesimal scalar. (3) implies that the plastic strain increment:
(d) The increment in plastic work per unit volume using (4.16) is:
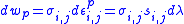 (4)
(4)
and the increment in strain energy, , equals to the total differential of the potential
, equals to the total differential of the potential  :
:
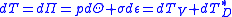 (5)
(5)
where
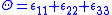 ,
, 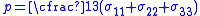 and for metals following the von Mises yield law, by definition
and for metals following the von Mises yield law, by definition
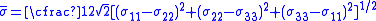 (6)
(6)
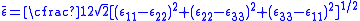 (7)
(7)
are the equivalent stress and strain respectively.
In (5) the first term of the right hand side, is the increment in elastic energy for unit volume change due to hydrostatic pressure. Its integral over a load path is the total amount of dilatational strain energy density stored in the material. The second term
is the increment in elastic energy for unit volume change due to hydrostatic pressure. Its integral over a load path is the total amount of dilatational strain energy density stored in the material. The second term 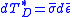 is the energy required for an infinitesimal distortion of the material. The integral of this quantity is the distortional strain energy density. The theory of plastic flow permits the evaluation of stresses, strains and strain energy densities along a path provided that
is the energy required for an infinitesimal distortion of the material. The integral of this quantity is the distortional strain energy density. The theory of plastic flow permits the evaluation of stresses, strains and strain energy densities along a path provided that  in (3) is known. In elasticity, linear or nonlinear,
in (3) is known. In elasticity, linear or nonlinear,  . In the case of strain hardening materials,
. In the case of strain hardening materials,  can be evaluated by recording the
can be evaluated by recording the 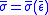 curve in a pure shear experiment. The hardening function after point “y” in Figure 1 is then:
curve in a pure shear experiment. The hardening function after point “y” in Figure 1 is then:
 (8)
(8)
and the infinitesimal scalar is:
is:
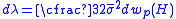 (9)
(9)
where is the infinitesimal increase in plastic work (see Figure 1). The elastic part of the total distortional strain energy density is:
is the infinitesimal increase in plastic work (see Figure 1). The elastic part of the total distortional strain energy density is:
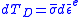 (10)
(10)
where is the elastic part of the equivalent strain. When there is no nonlinear elastic behaviour, by integrating (4.22) the elastic distortional strain energy density is:
is the elastic part of the equivalent strain. When there is no nonlinear elastic behaviour, by integrating (4.22) the elastic distortional strain energy density is:
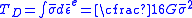 (11)
(11)
Similarly, by integrating the increment in elastic energy for unit volume change due to hydrostatic pressure, , the dilatational strain energy density is:
, the dilatational strain energy density is:
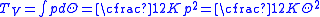 (12)
(12)
assuming that the unit volume change is the elastic straining, proportional to the hydrostatic pressure, p (Figure 2):
is the elastic straining, proportional to the hydrostatic pressure, p (Figure 2):
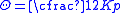 or
or  (13)
(13)
where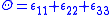 ,
, 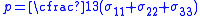 and
and 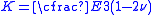 the bulk modulus of the material.
the bulk modulus of the material.
In summary, in order to use (12) and (13) to determine the failure of a material volume, the following assumptions hold:
 and
and 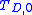 are derived from experimental data. A drawback of the criterion is that elastic strain energy densities are small and comparatively hard to derive. Nevertheless, example values are presented in the literature as well as applications where the T-criterion appears to perform quite well.
are derived from experimental data. A drawback of the criterion is that elastic strain energy densities are small and comparatively hard to derive. Nevertheless, example values are presented in the literature as well as applications where the T-criterion appears to perform quite well.
Failure theory (material)
Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure or ductile failure . Depending on the conditions most materials can fail in a brittle or ductile...
, that can be used to predict both brittle
Brittle
A material is brittle if, when subjected to stress, it breaks without significant deformation . Brittle materials absorb relatively little energy prior to fracture, even those of high strength. Breaking is often accompanied by a snapping sound. Brittle materials include most ceramics and glasses ...
and ductile failure. These criteria were designed as a replacement for the von Mises yield criterion which predicts the unphysical result that pure hydrostatic tensile loading of metals never leads to failure. The T-criteria use the volumetric stress in addition to the deviatoric stress used by the von Mises criterion and are similar to the Drucker Prager yield criterion
Drucker Prager yield criterion
The Drucker–Prager yield criterion is a pressure-dependent model for determining whether a material has failed or undergone plastic yielding. The criterion was introduced to deal with the plastic deformation of soils...
. T-criteria have been designed on the basis of energy considerations and the observation that the reversible elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
storage process has a limit which can be used to determine when a material has failed.
The strain energy density stored in the material and calculated by the area under the
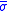 -
-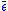 curve represents the total amount of energy stored in the material only in the case of pure shear. In all other cases, there is a divergence between the actual and calculated stored energy in the material, which is maximum in the case of pure hydrostatic loading, where, according to the von Mises criterion, no energy is stored. This paradox is resolved if a second constitutive equation is introduced, that relates hydrostatic pressure p with the volume change
curve represents the total amount of energy stored in the material only in the case of pure shear. In all other cases, there is a divergence between the actual and calculated stored energy in the material, which is maximum in the case of pure hydrostatic loading, where, according to the von Mises criterion, no energy is stored. This paradox is resolved if a second constitutive equation is introduced, that relates hydrostatic pressure p with the volume change  . These two curves, namely
. These two curves, namely  and (p-
and (p- ) are essential for a complete description of material behaviour up to failure. Thus, two criteria must be accounted for when considering failure and two constitutive equations that describe material response. According to this criterion, an upper limit to allowable strains is set either by a critical value ΤV,0 of the elastic energy density due to volume change (dilatational energy) or by a critical value ΤD,0 of the elastic energy density due to change in shape (distortional energy). The volume of material is considered to have failed by extensive plastic flow when the distortional energy Τd reaches the critical value ΤD,0 or by extensive dilatation when the dilatational energy Τv reaches a critical value ΤV,0. The two critical values ΤD,0 and ΤV,0 are considered material constants independent of the shape of the volume of material considered and the induced loading, but dependent on the strain rate and temperature.
) are essential for a complete description of material behaviour up to failure. Thus, two criteria must be accounted for when considering failure and two constitutive equations that describe material response. According to this criterion, an upper limit to allowable strains is set either by a critical value ΤV,0 of the elastic energy density due to volume change (dilatational energy) or by a critical value ΤD,0 of the elastic energy density due to change in shape (distortional energy). The volume of material is considered to have failed by extensive plastic flow when the distortional energy Τd reaches the critical value ΤD,0 or by extensive dilatation when the dilatational energy Τv reaches a critical value ΤV,0. The two critical values ΤD,0 and ΤV,0 are considered material constants independent of the shape of the volume of material considered and the induced loading, but dependent on the strain rate and temperature.Deployment for Isotropic Metals
For the development of the criterion, a continuum mechanics approach is adopted. The material volume is considered to be a continuous medium with no particular form or manufacturing defect. It is also considered to behave as a linear elastic isotropically hardening material, where stresses and strains are related by the generalised Hook’s law and by the incremental theory of plasticity with the von Mises flow rule. For such materials, the following assumptions are considered to hold:(a) The total increment of a strain component
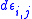 is decomposed into the elastic and the plastic
is decomposed into the elastic and the plastic  increment and
increment and  respectively:
respectively: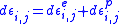 (1)
(1)(b) The elastic strain increment
 is given by Hooke’s law:
is given by Hooke’s law: (2)
(2)where
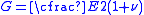 the shear modulus,
the shear modulus,  the Poisson’s ratio and
the Poisson’s ratio and 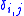 the Krönecker delta.
the Krönecker delta.(c) The plastic strain increment
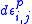 is proportional to the respective deviatoric stress:
is proportional to the respective deviatoric stress: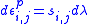 (3)
(3)where
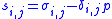 and
and  an infinitesimal scalar. (3) implies that the plastic strain increment:
an infinitesimal scalar. (3) implies that the plastic strain increment:
- depends on the value of stresses, not on their variation
- is independent of the hydrostatic component of the stress tensor
- is collinear with the deviatoric stresses (isotropic material)
(d) The increment in plastic work per unit volume using (4.16) is:
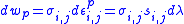 (4)
(4)and the increment in strain energy,
 , equals to the total differential of the potential
, equals to the total differential of the potential  :
: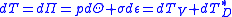 (5)
(5)where
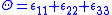 ,
, 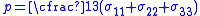 and for metals following the von Mises yield law, by definition
and for metals following the von Mises yield law, by definition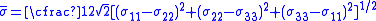 (6)
(6)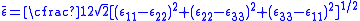 (7)
(7)are the equivalent stress and strain respectively.
In (5) the first term of the right hand side,
 is the increment in elastic energy for unit volume change due to hydrostatic pressure. Its integral over a load path is the total amount of dilatational strain energy density stored in the material. The second term
is the increment in elastic energy for unit volume change due to hydrostatic pressure. Its integral over a load path is the total amount of dilatational strain energy density stored in the material. The second term 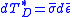 is the energy required for an infinitesimal distortion of the material. The integral of this quantity is the distortional strain energy density. The theory of plastic flow permits the evaluation of stresses, strains and strain energy densities along a path provided that
is the energy required for an infinitesimal distortion of the material. The integral of this quantity is the distortional strain energy density. The theory of plastic flow permits the evaluation of stresses, strains and strain energy densities along a path provided that  in (3) is known. In elasticity, linear or nonlinear,
in (3) is known. In elasticity, linear or nonlinear,  . In the case of strain hardening materials,
. In the case of strain hardening materials,  can be evaluated by recording the
can be evaluated by recording the 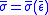 curve in a pure shear experiment. The hardening function after point “y” in Figure 1 is then:
curve in a pure shear experiment. The hardening function after point “y” in Figure 1 is then: (8)
(8)and the infinitesimal scalar
 is:
is: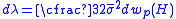 (9)
(9)where
 is the infinitesimal increase in plastic work (see Figure 1). The elastic part of the total distortional strain energy density is:
is the infinitesimal increase in plastic work (see Figure 1). The elastic part of the total distortional strain energy density is: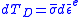 (10)
(10)where
 is the elastic part of the equivalent strain. When there is no nonlinear elastic behaviour, by integrating (4.22) the elastic distortional strain energy density is:
is the elastic part of the equivalent strain. When there is no nonlinear elastic behaviour, by integrating (4.22) the elastic distortional strain energy density is: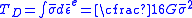 (11)
(11)Similarly, by integrating the increment in elastic energy for unit volume change due to hydrostatic pressure,
 , the dilatational strain energy density is:
, the dilatational strain energy density is: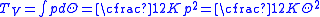 (12)
(12)assuming that the unit volume change
 is the elastic straining, proportional to the hydrostatic pressure, p (Figure 2):
is the elastic straining, proportional to the hydrostatic pressure, p (Figure 2):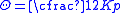 or
or  (13)
(13)where
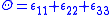 ,
, 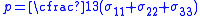 and
and 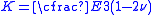 the bulk modulus of the material.
the bulk modulus of the material. In summary, in order to use (12) and (13) to determine the failure of a material volume, the following assumptions hold:
- The material is isotropic and follows the von Mises yield condition
- The elastic part of the stress-strain curve is linear
- The relationship between hydrostatic pressure and unit volume change is linear
- The derivative (hardening slope) must be positive or zero
Limitations
The criterion will not predict any failure due to distortion for elastic-perfectly plastic, rigid-plastic, or strain softening materials. For the case of nonlinear elasticity, appropriate calculations for the integrals in and (12) and (13) accounting for the nonlinear elastic material properties must be performed. The two threshold values for the elastic strain energy and
and 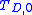 are derived from experimental data. A drawback of the criterion is that elastic strain energy densities are small and comparatively hard to derive. Nevertheless, example values are presented in the literature as well as applications where the T-criterion appears to perform quite well.
are derived from experimental data. A drawback of the criterion is that elastic strain energy densities are small and comparatively hard to derive. Nevertheless, example values are presented in the literature as well as applications where the T-criterion appears to perform quite well.

