Tait's conjecture
Encyclopedia
In mathematics, Tait's conjecture states that "Every 3-connected
planar
cubic graph
has a Hamiltonian cycle (along the edges) through all its vertices
". It was proposed by and disproved by , who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by .
The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron
, which forms a bipartite graph
with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.
The conjecture could have been significant, because if true, it would have implied the four color theorem
: as Tait described, the four-color problem is equivalent to the problem of finding 3-edge-colorings
of bridgeless cubic planar graphs. In a Hamiltonian cubic planar graph, such an edge coloring is easy to find: use two colors alternately on the cycle, and a third color for all remaining edges. Alternatively, a 4-coloring of the faces of a Hamiltonian cubic planar graph may be constructed directly, using two colors for the faces inside the cycle and two more colors for the faces outside.
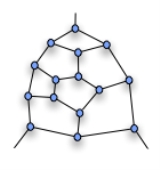
If this fragment is part of a larger graph, then any Hamiltonian cycle through the graph must go in or out of the top vertex (and either one of the lower ones). It cannot go in one lower vertex and out the other.
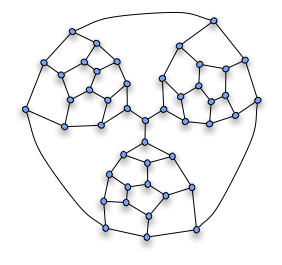
The fragment can then be used to construct the non-Hamiltonian Tutte graph
, by putting
together three such fragments as shown on the picture. The "compulsory" edges of the fragments, that must be part of any Hamiltonian path through the fragment, are connected together at the central vertex; because any cycle can use only two of these three edges, there can be no Hamiltonian cycle.
The resulting Tutte graph
is 3-connected and planar
, so by Steinitz' theorem
it is the graph of a polyhedron. In total it has 25 faces, 69 edges and 46 vertices.
It can be realized geometrically from a tetrahedron (the faces of which correspond to the four large faces in the drawing, three of which are between pairs of fragments and the fourth of which forms the exterior) by multiply truncating three of its vertices.
by the same fragment used in Tutte's example.
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
has a Hamiltonian cycle (along the edges) through all its vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
". It was proposed by and disproved by , who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by .
The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, which forms a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.
The conjecture could have been significant, because if true, it would have implied the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
: as Tait described, the four-color problem is equivalent to the problem of finding 3-edge-colorings
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
of bridgeless cubic planar graphs. In a Hamiltonian cubic planar graph, such an edge coloring is easy to find: use two colors alternately on the cycle, and a third color for all remaining edges. Alternatively, a 4-coloring of the faces of a Hamiltonian cubic planar graph may be constructed directly, using two colors for the faces inside the cycle and two more colors for the faces outside.
Tutte's fragment
The key to this counter-example is what is now known as Tutte's fragment, shown to the right.If this fragment is part of a larger graph, then any Hamiltonian cycle through the graph must go in or out of the top vertex (and either one of the lower ones). It cannot go in one lower vertex and out the other.
The counterexample

The fragment can then be used to construct the non-Hamiltonian Tutte graph
Tutte graph
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8....
, by putting
together three such fragments as shown on the picture. The "compulsory" edges of the fragments, that must be part of any Hamiltonian path through the fragment, are connected together at the central vertex; because any cycle can use only two of these three edges, there can be no Hamiltonian cycle.
The resulting Tutte graph
Tutte graph
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8....
is 3-connected and planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, so by Steinitz' theorem
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
it is the graph of a polyhedron. In total it has 25 faces, 69 edges and 46 vertices.
It can be realized geometrically from a tetrahedron (the faces of which correspond to the four large faces in the drawing, three of which are between pairs of fragments and the fourth of which forms the exterior) by multiply truncating three of its vertices.
Smaller counterexamples
As show, there are exactly six 38-vertex non-Hamiltonian polyhedra that have nontrivial three-edge cuts. They are formed by replacing two of the vertices of a pentagonal prismPentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
by the same fragment used in Tutte's example.
See also
- Grinberg's theoremGrinberg's theoremIn graph theory, Grinberg's theorem is a necessary condition on the planar graph to contain a Hamiltonian cycle. The result has been widely used to construct non-Hamiltonian planar graphs with further properties, such as to give new counterexamples to Tait's conjecture...
, a necessary condition on the existence of a Hamiltonian cycle that can be used to show that a graph forms a counterexample to Tait's conjecture - Barnette's conjectureBarnette's conjectureBarnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W...
, a still-open refinement of Tait's conjecture stating that every bipartiteBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
cubic polyhedral graphPolyhedral graphIn polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
is Hamiltonian.

