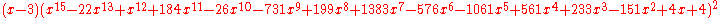Tutte graph
Encyclopedia
In the mathematical
field of graph theory
, the Tutte graph is a 3-regular graph
with 46 vertices and 69 edges named after W. T. Tutte
. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.
The Tutte graph is a cubic
polyhedral graph
, but is non-hamiltonian. Therefore, it is a counterexample to the Tait's conjecture
that every 3-regular polyhedron has a Hamiltonian cycle.
Published by Tutte in 1946, it is the first counterexample constructed for this conjecture. Other counterexamples were found later.
constructed a non-Hamiltonian polyhedron, by putting together three such fragments. The "compulsory" edges of the fragments, that must be part of any Hamiltonian path through the fragment, are connected together at the central vertex; because any cycle can use only two of these three edges, there can be no Hamiltonian cycle.
The resulting graph is 3-connected and planar
, so by Steinitz' theorem
it is the graph of a polyhedron. It has 25 faces.
It can be realized geometrically from a tetrahedron (the faces of which correspond to the four large nine-sided faces in the drawing, three of which are between pairs of fragments and the fourth of which forms the exterior) by multiply truncating three of its vertices.
of order 3.
The characteristic polynomial
of the Tutte graph is :
In 1965 Lederberg found the Barnette-Bosák-Lederberg graph on 38 vertices. In 1968, Grinberg constructed additional small counterexamples to the Tait's conjecture - the Grinberg graphs on 42, 44 and 46 vertices. In 1974 Faulkner and Younger published two more graphs - the Faulkner-Younger graphs on 42 and 44 vertices.
Finally Holton and McKay showed there are exactly six 38-vertex non-Hamiltonian polyhedra that have nontrivial three-edge cuts. They are formed by replacing two of the vertices of a pentagonal prism
by the same fragment used in Tutte's example.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Tutte graph is a 3-regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
with 46 vertices and 69 edges named after W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.
The Tutte graph is a cubic
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
, but is non-hamiltonian. Therefore, it is a counterexample to the Tait's conjecture
Tait's conjecture
In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by and disproved by , who constructed a counterexample with 25 faces, 69 edges and 46 vertices...
that every 3-regular polyhedron has a Hamiltonian cycle.
Published by Tutte in 1946, it is the first counterexample constructed for this conjecture. Other counterexamples were found later.
Construction
From a small planar graph called the Tutte fragment, W. T. TutteW. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
constructed a non-Hamiltonian polyhedron, by putting together three such fragments. The "compulsory" edges of the fragments, that must be part of any Hamiltonian path through the fragment, are connected together at the central vertex; because any cycle can use only two of these three edges, there can be no Hamiltonian cycle.
The resulting graph is 3-connected and planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, so by Steinitz' theorem
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
it is the graph of a polyhedron. It has 25 faces.
It can be realized geometrically from a tetrahedron (the faces of which correspond to the four large nine-sided faces in the drawing, three of which are between pairs of fragments and the fourth of which forms the exterior) by multiply truncating three of its vertices.
Algebraic properties
The automorphism group of the Tutte graph is Z/3Z, the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 3.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Tutte graph is :
Related graphs
Although the Tutte graph is the first 3-regular non-Hamiltonian polyhedral graph to be discovered, it is not the smallest such graph.In 1965 Lederberg found the Barnette-Bosák-Lederberg graph on 38 vertices. In 1968, Grinberg constructed additional small counterexamples to the Tait's conjecture - the Grinberg graphs on 42, 44 and 46 vertices. In 1974 Faulkner and Younger published two more graphs - the Faulkner-Younger graphs on 42 and 44 vertices.
Finally Holton and McKay showed there are exactly six 38-vertex non-Hamiltonian polyhedra that have nontrivial three-edge cuts. They are formed by replacing two of the vertices of a pentagonal prism
Pentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
by the same fragment used in Tutte's example.