
Tanh-sinh quadrature
Encyclopedia
Tanh-sinh quadrature is a method for numerical integration
introduced by Hidetosi Takahasi and Masatake Mori in 1974. It uses the change of variables

to transform an integral on the interval x ∈ (−1, +1) to an integral on the entire real line
t ∈ (−∞,+∞). After this transformation, the integrand decays with a double exponential rate, and thus, this method is also known as the double exponential (DE) formula.
For a given step size h, the integral is approximated by the sum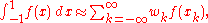
with the abscissas
and the weights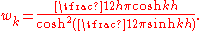
Like Gaussian quadrature
, tanh-sinh quadrature is well suited for arbitrary-precision
integration, where an accuracy of hundreds or even thousands of digits is desired. The convergence is quadratic for sufficiently well-behaved integrands: doubling the number of evaluation points roughly doubles the number of correct digits.
Tanh-sinh quadrature is less efficient than Gaussian quadrature for smooth integrands, but unlike Gaussian quadrature tends to work equally well with integrands having singularities or infinite derivatives at one or both endpoints of the integration interval. A further advantage is that the abscissas and weights are relatively easy to compute. The cost of calculating abscissa-weight pairs for n-digit accuracy is roughly n2 log2 n compared to n3 log n for Gaussian quadrature.
Upon comparing the scheme to Gaussian quadrature and error function quadrature, Bailey et al. (2005) found that the tanh-sinh scheme "appears to be the best for integrands of the type most often encountered in experimental math research".
Bailey and others have done extensive research on tanh-sinh quadrature, Gaussian quadrature and error function quadrature, as well as several of the classical quadrature methods, and found that the classical methods are not competitive with the first three methods, particularly when high-precision results are required. In a conference paper (July 2004) comparing tanh-sinh quadrature with Gaussian quadrature and error function quadrature, Bailey and Li found: "Overall, the tanh-sinh scheme appears to be the best. It combines uniformly excellent accuracy with fast run times. It is the nearest we have to a truly all-purpose quadrature scheme at the present time."
Bailey (2006) found that: "The tanh-sinh quadrature scheme is the fastest known high-precision quadrature scheme, especially when the time for computing abscissas and weights is considered. It has been successfully employed for quadrature calculations of up to 20,000-digit precision. It works well for functions with blow-up singularities or infinite derivatives at endpoints."
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
introduced by Hidetosi Takahasi and Masatake Mori in 1974. It uses the change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...

to transform an integral on the interval x ∈ (−1, +1) to an integral on the entire real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
t ∈ (−∞,+∞). After this transformation, the integrand decays with a double exponential rate, and thus, this method is also known as the double exponential (DE) formula.
For a given step size h, the integral is approximated by the sum
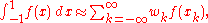
with the abscissas

and the weights
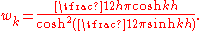
Like Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
, tanh-sinh quadrature is well suited for arbitrary-precision
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
integration, where an accuracy of hundreds or even thousands of digits is desired. The convergence is quadratic for sufficiently well-behaved integrands: doubling the number of evaluation points roughly doubles the number of correct digits.
Tanh-sinh quadrature is less efficient than Gaussian quadrature for smooth integrands, but unlike Gaussian quadrature tends to work equally well with integrands having singularities or infinite derivatives at one or both endpoints of the integration interval. A further advantage is that the abscissas and weights are relatively easy to compute. The cost of calculating abscissa-weight pairs for n-digit accuracy is roughly n2 log2 n compared to n3 log n for Gaussian quadrature.
Upon comparing the scheme to Gaussian quadrature and error function quadrature, Bailey et al. (2005) found that the tanh-sinh scheme "appears to be the best for integrands of the type most often encountered in experimental math research".
Bailey and others have done extensive research on tanh-sinh quadrature, Gaussian quadrature and error function quadrature, as well as several of the classical quadrature methods, and found that the classical methods are not competitive with the first three methods, particularly when high-precision results are required. In a conference paper (July 2004) comparing tanh-sinh quadrature with Gaussian quadrature and error function quadrature, Bailey and Li found: "Overall, the tanh-sinh scheme appears to be the best. It combines uniformly excellent accuracy with fast run times. It is the nearest we have to a truly all-purpose quadrature scheme at the present time."
Bailey (2006) found that: "The tanh-sinh quadrature scheme is the fastest known high-precision quadrature scheme, especially when the time for computing abscissas and weights is considered. It has been successfully employed for quadrature calculations of up to 20,000-digit precision. It works well for functions with blow-up singularities or infinite derivatives at endpoints."
External links
- John D. Cook, "Double Exponential Integration" with source code.
- Graeme Dennes, " Tanh-Sinh Quadrature V2.1" A Microsoft Excel workbook containing three functions for performing Tanh-Sinh, Gauss–Kronrod and RombergRomberg's methodIn numerical analysis, Romberg's method is used to estimate the definite integral \int_a^b f \, dx by applying Richardson extrapolation repeatedly on the trapezium rule or the rectangle rule . The estimates generate a triangular array...
numerical integration of functions over the finite interval (a,b), and two functions for performing double exponential (DE) numerical integration of functions over the semi-infinite interval (a,∞), for oscillatory and non-oscillatory functions. Demonstrates the astounding speed and accuracy of the Tanh-Sinh method in particular and the double exponential methods in general, all of which are members of the family of double-exponential quadrature techniques developed by Takahasi and Mori in 1974. Full open source code is provided, including extensive documentation.

