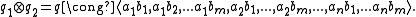Tensor product of quadratic forms
Encyclopedia
The tensor product
of quadratic form
s is most easily understood when one views the quadratic forms as quadratic spaces. So, if (V, q1) and (W, q2) are quadratic spaces, which V,W vector spaces, then the tensor product is a quadratic form q on the tensor product of vector spaces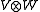 .
.
It is defined in such a way that for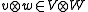 we have
we have 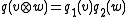 . In particular, if we have diagonalizations of our quadratic forms (which is always possible when the characteristic
. In particular, if we have diagonalizations of our quadratic forms (which is always possible when the characteristic
is not 2) such that
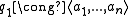
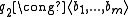
then the tensor product has diagonalization
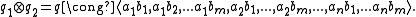
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s is most easily understood when one views the quadratic forms as quadratic spaces. So, if (V, q1) and (W, q2) are quadratic spaces, which V,W vector spaces, then the tensor product is a quadratic form q on the tensor product of vector spaces
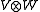 .
.It is defined in such a way that for
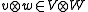 we have
we have 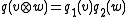 . In particular, if we have diagonalizations of our quadratic forms (which is always possible when the characteristic
. In particular, if we have diagonalizations of our quadratic forms (which is always possible when the characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is not 2) such that
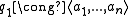
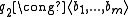
then the tensor product has diagonalization