
Term test
Encyclopedia
In mathematics
, the nth term test for divergence is a simple test for the divergence
of an infinite series:
Many authors do not name this test or give it a shorter name.
, the term test cannot prove by itself that a series converges. In particular, the converse to the test is not true; instead all one can say is:
The harmonic series
is a classic example of a divergent series whose terms limit to zero. The more general class of p-series
,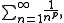
exemplifies the possible results of the test:
converges means that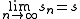
for some number s. Then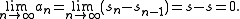
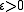 there is a number N such that
there is a number N such that
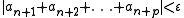
holds for all n > N and p ≥ 1. Setting p = 1 recovers the definition of the statement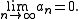
s. The above two proofs, by invoking the Cauchy criterion or the linearity of the limit, also work in any other normed vector space
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the nth term test for divergence is a simple test for the divergence
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
of an infinite series:
- If
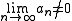 or if the limit does not exist, then
or if the limit does not exist, then 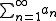 diverges.
diverges.
Many authors do not name this test or give it a shorter name.
Usage
Unlike stronger convergence testsConvergence tests
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series.- List of tests :...
, the term test cannot prove by itself that a series converges. In particular, the converse to the test is not true; instead all one can say is:
- If
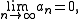 then
then 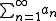 may or may not converge. In other words, if
may or may not converge. In other words, if  , the test is inconclusive.
, the test is inconclusive.
The harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
is a classic example of a divergent series whose terms limit to zero. The more general class of p-series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
,
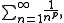
exemplifies the possible results of the test:
- If p ≤ 0, then the term test identifies the series as divergent.
- If 0 < p ≤ 1, then the term test is inconclusive, but the series is divergent by the integral test for convergenceIntegral test for convergenceIn mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
. - If 1 < p, then the term test is inconclusive, but the series is convergent, again by the integral test for convergence.
Proofs
The test is typically proved in contrapositive form:- If
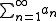 converges, then
converges, then 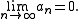
Limit manipulation
If sn are the partial sums of the series, then the assumption that the seriesconverges means that
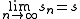
for some number s. Then
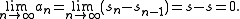
Cauchy's criterion
The assumption that the series converges means that it passes Cauchy's convergence test: for every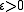 there is a number N such that
there is a number N such that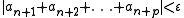
holds for all n > N and p ≥ 1. Setting p = 1 recovers the definition of the statement
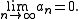
Scope
The simplest version of the term test applies to infinite series of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The above two proofs, by invoking the Cauchy criterion or the linearity of the limit, also work in any other normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
.

