
The Beauty of Fractals
Encyclopedia
The Beauty of Fractals is a 1986 book by Heinz-Otto Peitgen
and Peter Richter which publicises the fields of complex dynamics
, chaos theory
and the concept of fractal
s. It is lavishly illustrated and as a mathematics book became an unusual success.
The book includes a total of 184 illustrations, including 88 full-colour pictures of Julia sets. Although the format suggests a coffee table book
, the discussion of the background of the presented images addresses some sophisticated mathematics which would not be found in popular science books. In 1987 the book won an Award for distinguished technical communication.
, Chaos
and Fractals. In particular the Feigenbaum
scenario and the relation to Julia Sets and the Mandelbrot set
is discussed. The following special sections provide in depth detail for the shown images: Verhulst Dynamics, Julia Sets and Their Computergraphical Generation, Sullivan's Classification of Critical Points, The Mandelbrot Set, External Angles and Hubbard Trees, Newton's Method for Complex Polynomials: Cayley's Problem, Newtons's Method for Real Equations, A Discrete Volterra-Lotka System, Yang-Lee Zeros, Renormalization (Magnetism and Complex Boundaries).
The book also includes invited Contributions by Benoît Mandelbrot
, Adrien Douady
, Gert Eilenberger and Herbert W. Franke
, which provide additional formality and some historically interesting detail. Benoit Mandelbrot gives a very personal account of his discovery of fractals in general and the fractal named after him in particular. Adrien Douady explains the solved and unsolved problems relating to the almost amusingly complex Mandelbrot set.
The book was cited and its images were reproduced in a number of publications. Some images were even used before the book was published. The cover article of the Scientific American August 1985 edition showed some the images and provided reference to the book to be published.
One particular image sequence of the book is the close up series "seahorse valley". While the first publication of such a close up series was the June 1984 cover article of the Magazine Geo, The Beauty of Fractals provided the first such publication within a book.
Heinz-Otto Peitgen
thumb|180px|right|Heinz-Otto PeitgenHeinz-Otto Peitgen is a German mathematician. Peitgen is one of the most prominent researchers in the study of fractals.- Life :...
and Peter Richter which publicises the fields of complex dynamics
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and the concept of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s. It is lavishly illustrated and as a mathematics book became an unusual success.
The book includes a total of 184 illustrations, including 88 full-colour pictures of Julia sets. Although the format suggests a coffee table book
Coffee table book
A coffee table book is a hardcover book that is intended to sit on a coffee table or similar surface in an area where guests sit and are entertained, thus inspiring conversation or alleviating boredom. They tend to be oversized and of heavy construction, since there is no pressing need for...
, the discussion of the background of the presented images addresses some sophisticated mathematics which would not be found in popular science books. In 1987 the book won an Award for distinguished technical communication.
Summary
The books starts with a general introduction to Complex DynamicsDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, Chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and Fractals. In particular the Feigenbaum
Mitchell Feigenbaum
Mitchell Jay Feigenbaum is a mathematical physicist whose pioneering studies in chaos theory led to the discovery of the Feigenbaum constants.- Biography :...
scenario and the relation to Julia Sets and the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
is discussed. The following special sections provide in depth detail for the shown images: Verhulst Dynamics, Julia Sets and Their Computergraphical Generation, Sullivan's Classification of Critical Points, The Mandelbrot Set, External Angles and Hubbard Trees, Newton's Method for Complex Polynomials: Cayley's Problem, Newtons's Method for Real Equations, A Discrete Volterra-Lotka System, Yang-Lee Zeros, Renormalization (Magnetism and Complex Boundaries).
The book also includes invited Contributions by Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
, Adrien Douady
Adrien Douady
Adrien Douady was a French mathematician.He was a student of Henri Cartan at the Ecole Normale Supérieure, and initially worked in homological algebra. His thesis concerned deformations of complex analytic spaces...
, Gert Eilenberger and Herbert W. Franke
Herbert W. Franke
Herbert W. Franke is an Austrian scientist and writer. He is considered one of the most important science fiction authors in the German language....
, which provide additional formality and some historically interesting detail. Benoit Mandelbrot gives a very personal account of his discovery of fractals in general and the fractal named after him in particular. Adrien Douady explains the solved and unsolved problems relating to the almost amusingly complex Mandelbrot set.
The images
Part of the text was originally conceived as a supplemented catalogue to the exhibition Frontiers of Chaos of the German Goethe-Institut, first seen in Europe and the United States. It described the context and meaning of these images. The images were created at the "Computer Graphics Laboratory Dynamical Systems" at the University of Bremen in 1984 and 1985. Dedicated software had to be developed to make the necessary computations which at that time took hours of computer time to create a single image. For the exhibit and the book the computed images had to be captured as photographs. Digital image capturing and archiving were not feasible at that time.The book was cited and its images were reproduced in a number of publications. Some images were even used before the book was published. The cover article of the Scientific American August 1985 edition showed some the images and provided reference to the book to be published.
One particular image sequence of the book is the close up series "seahorse valley". While the first publication of such a close up series was the June 1984 cover article of the Magazine Geo, The Beauty of Fractals provided the first such publication within a book.
 Start of the zoom |
 Step 2a (Central Spiral) |
 Step 2 (Part of Tail) |
 Step 3 |
 Julia Set |
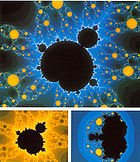 Potts Model, q-plane |
 Newton Iteration |
Translations
- Italian translation: La Bellezza dei Frattali, Bollati Boringhieri, Torino 1987, ISBN 88-339-0420-2
- Japanese translation: Springer-Verlag, Tokyo 1988, ISBN 3-540-15851-0
- Russian translation: Krasota Fractalov, Mir, Moscow 1993, ISBN 5-03-001296-6
- Chinese translation: Z.-J. Jing and X.-S. Zhang, Science Publishers, Beijing 1994, ISBN 7-03-004188-7/TP 374

