
Mitchell Feigenbaum
Encyclopedia
Mitchell Jay Feigenbaum (born December 19, 1944) is a mathematical physicist
whose pioneering studies in chaos theory
led to the discovery of the Feigenbaum constants
.
, to Polish
and Ukrainian
Jewish immigrants. He attended Samuel J. Tilden High School
, in Brooklyn
, New York, and the City College of New York
. In 1964 he began his graduate studies at the Massachusetts Institute of Technology
(MIT). Enrolling for graduate study in electrical engineering
, he changed his area to physics
. He completed his doctorate in 1970 for a thesis on dispersion relation
s, under the supervision of Professor Francis E. Low
.
After short positions at Cornell University
and the Virginia Polytechnic Institute, he was offered a longer-term post at the Los Alamos National Laboratory
in New Mexico
to study turbulence
in fluids. Although that group of researchers was ultimately unable to unravel the currently intractable theory of turbulent fluids, his research led him to study chaotic maps.
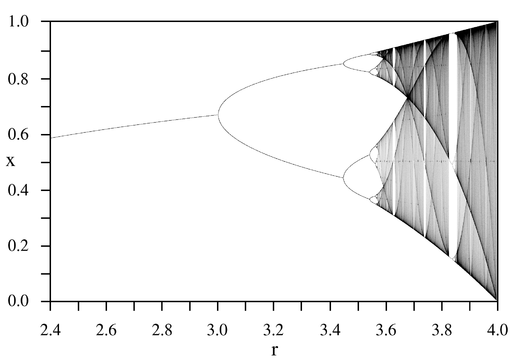
calculator he had been issued, discovered that the ratio of the difference between the values at which such successive period-doubling bifurcation
s occur tends to a constant of around 4.6692... He was able to provide a mathematical proof of that fact, and he then showed that the same behavior, with the same mathematical constant, would occur within a wide class of mathematical functions, prior to the onset of chaos. For the first time, this universal result enabled mathematicians to take their first steps to unraveling the apparently intractable "random" behavior of chaotic systems. This "ratio of convergence" is now known as the first Feigenbaum constant.
The Logistic map
is a prominent example of the mappings that Feigenbaum studied in his noted 1978 article: Quantitative Universality for a Class of Nonlinear Transformations.
Feigenbaum's other contributions include important new fractal
methods in cartography
, starting when he was hired by Hammond to develop techniques to allow computers to assist in drawing maps. The introduction to the Hammond Atlas (1992) states:
In 1983 he was awarded a MacArthur Fellowship
, and in 1986, he was awarded the Wolf Prize in Physics
"for his pioneering theoretical studies demonstrating the universal character of non-linear systems, which has made possible the systematic study of chaos". He is a member of the Board of Scientific Governors at The Scripps Research Institute
. He has been Toyota Professor at Rockefeller University
since 1986.
The press release made on the occasion of his receiving the Wolf Prize summed up his works:
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
whose pioneering studies in chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
led to the discovery of the Feigenbaum constants
Feigenbaum constants
The Feigenbaum constants are two mathematical constants named after the mathematician Mitchell Feigenbaum. Both express ratios in a bifurcation diagram.The first Feigenbaum constant ,...
.
Biography
Feigenbaum was born in New York CityNew York City
New York is the most populous city in the United States and the center of the New York Metropolitan Area, one of the most populous metropolitan areas in the world. New York exerts a significant impact upon global commerce, finance, media, art, fashion, research, technology, education, and...
, to Polish
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
and Ukrainian
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
Jewish immigrants. He attended Samuel J. Tilden High School
Samuel J. Tilden High School
Samuel J. Tilden High School is a New York City public high school in the East Flatbush section of Brooklyn. It is named for Samuel J. Tilden, the former governor of New York State and presidential candidate who, although carrying the popular vote, lost to Rutherford B...
, in Brooklyn
Brooklyn
Brooklyn is the most populous of New York City's five boroughs, with nearly 2.6 million residents, and the second-largest in area. Since 1896, Brooklyn has had the same boundaries as Kings County, which is now the most populous county in New York State and the second-most densely populated...
, New York, and the City College of New York
City College of New York
The City College of the City University of New York is a senior college of the City University of New York , in New York City. It is also the oldest of the City University's twenty-three institutions of higher learning...
. In 1964 he began his graduate studies at the Massachusetts Institute of Technology
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
(MIT). Enrolling for graduate study in electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, he changed his area to physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. He completed his doctorate in 1970 for a thesis on dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
s, under the supervision of Professor Francis E. Low
Francis E. Low
Francis Eugene Low was an American theoretical physicist. He was an Institute Professor at MIT, and served as provost there from 1980 to 1985.-Early career:...
.
After short positions at Cornell University
Cornell University
Cornell University is an Ivy League university located in Ithaca, New York, United States. It is a private land-grant university, receiving annual funding from the State of New York for certain educational missions...
and the Virginia Polytechnic Institute, he was offered a longer-term post at the Los Alamos National Laboratory
Los Alamos National Laboratory
Los Alamos National Laboratory is a United States Department of Energy national laboratory, managed and operated by Los Alamos National Security , located in Los Alamos, New Mexico...
in New Mexico
New Mexico
New Mexico is a state located in the southwest and western regions of the United States. New Mexico is also usually considered one of the Mountain States. With a population density of 16 per square mile, New Mexico is the sixth-most sparsely inhabited U.S...
to study turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
in fluids. Although that group of researchers was ultimately unable to unravel the currently intractable theory of turbulent fluids, his research led him to study chaotic maps.

Work
Some mathematical mappings involving a single linear parameter exhibit the apparently random behavior known as chaos when the parameter lies within certain ranges. As the parameter is increased towards this region, the mapping undergoes bifurcations at precise values of the parameter. At first there is one stable point, then bifurcating to an oscillation between two values, then bifurcating again to oscillate between four values and so on. In 1975, Dr. Feigenbaum, using the small HP-65HP-65
The HP-65 was the first magnetic card-programmable handheld calculator. Introduced by Hewlett-Packard in 1974 at an MSRP of $795, it featured nine storage registers and room for 100 keystroke instructions. It also included a magnetic card reader/writer to save and load programs...
calculator he had been issued, discovered that the ratio of the difference between the values at which such successive period-doubling bifurcation
Period-doubling bifurcation
In mathematics, a period doubling bifurcation in a discrete dynamical system is a bifurcation in which the system switches to a new behavior with twice the period of the original system...
s occur tends to a constant of around 4.6692... He was able to provide a mathematical proof of that fact, and he then showed that the same behavior, with the same mathematical constant, would occur within a wide class of mathematical functions, prior to the onset of chaos. For the first time, this universal result enabled mathematicians to take their first steps to unraveling the apparently intractable "random" behavior of chaotic systems. This "ratio of convergence" is now known as the first Feigenbaum constant.
The Logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
is a prominent example of the mappings that Feigenbaum studied in his noted 1978 article: Quantitative Universality for a Class of Nonlinear Transformations.
Feigenbaum's other contributions include important new fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
methods in cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
, starting when he was hired by Hammond to develop techniques to allow computers to assist in drawing maps. The introduction to the Hammond Atlas (1992) states:
"Using fractal geometry to describe natural forms such as coastlines, mathematical physicist Mitchell Feigenbaum developed software capable reconfiguring coastlines, borders, and mountain ranges to fit a multitude of map scales and projections. Dr. Feigenbaum also created a new computerized type placement program which places thousands of map labels in minutes, a task which previously required days of tedious labor."
In 1983 he was awarded a MacArthur Fellowship
MacArthur Foundation
The John D. and Catherine T. MacArthur Foundation is one of the largest private foundations in the United States. Based in Chicago but supporting non-profit organizations that work in 60 countries, MacArthur has awarded more than US$4 billion since its inception in 1978...
, and in 1986, he was awarded the Wolf Prize in Physics
Wolf Prize in Physics
The Wolf Prize in Physics is awarded once a year by the Wolf Foundation in Israel. It is one of the six Wolf Prizes established by the Foundation and awarded since 1978; the others are in Agriculture, Chemistry, Mathematics, Medicine and Arts. The Prize is often considered the most prestigious...
"for his pioneering theoretical studies demonstrating the universal character of non-linear systems, which has made possible the systematic study of chaos". He is a member of the Board of Scientific Governors at The Scripps Research Institute
The Scripps Research Institute
The Scripps Research Institute is an American medical research facility that focuses on research in the basic biomedical sciences. Headquartered in La Jolla, California, with a sister facility in Jupiter, Florida, the institute is home to 3,000 scientists, technicians, graduate students, and...
. He has been Toyota Professor at Rockefeller University
Rockefeller University
The Rockefeller University is a private university offering postgraduate and postdoctoral education. It has a strong concentration in the biological sciences. It is also known for producing numerous Nobel laureates...
since 1986.
The press release made on the occasion of his receiving the Wolf Prize summed up his works:
"The impact of Feigenbaum's discoveries has been phenomenal. It has spanned new fields of theoretical and experimental mathematics ... It is hard to think of any other development in recent theoretical science that has had so broad an impact over so wide a range of fields, spanning both the very pure and the very applied."
In popular culture
- In the AngelAngel (TV series)Angel is an American television series, a spin-off of the television series Buffy the Vampire Slayer. The series was created by Buffys creator, Joss Whedon, in collaboration with David Greenwalt, and first aired on October 5, 1999...
(TV series) episode, "A Hole in the World", doctoral candidate Winifred "Fred" BurkleWinifred BurkleWinifred "Fred" Burkle is a fictional character created by Joss Whedon and introduced by Shawn Ryan and Mere Smith on the television series Angel. The character is portrayed by Amy Acker.-Character history:...
(portrayed by Amy AckerAmy AckerAmy Louise Acker is an American actress. She is best known for her roles on the television series Angel as Winifred Burkle and Illyria and on Alias as Kelly Peyton. She is also known for her role as Dr. Claire Saunders/Whiskey on Dollhouse.-Early life:Acker was born and raised in Dallas, where she...
) is shown to have a stuffed bunny named Feigenbaum (whom she refers to as the "master of chaos").
See also
- Chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
- FractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
- Logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
- Theory of Colours (book)

