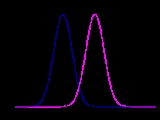
Radial basis function
Encyclopedia
A radial basis function is a real-valued function whose value depends only on the distance from the origin
, so that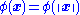
; or alternatively on the distance from some other point c, called a center, so that 
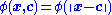. Any function 
that satisfies the property 
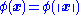is a radial function. The norm is usually Euclidean distance
, although other distance functions are also possible. For example by using Lukaszyk-Karmowski metric
, it is possible for some radial functions to avoid problems with ill conditioning
of the matrix solved to determine coefficients wi (see below), since the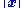
is always greater than zero.
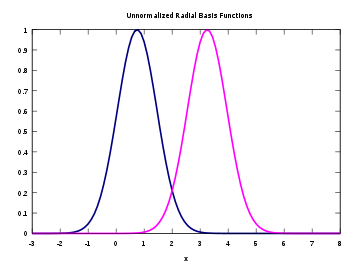
Sums of radial basis functions are typically used to approximate given functions
. This approximation process can also be interpreted as a simple kind of neural network
.
):
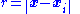s of the form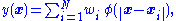
where the approximating function y(x) is represented as a sum of N radial basis functions, each associated with a different center xi, and weighted by an appropriate coefficient wi. The weights wi can be estimated using the matrix methods of linear least squares
, because the approximating function is linear in the weights.
Approximation schemes of this kind have been particularly used in time series prediction and control
of nonlinear systems exhibiting sufficiently simple chaotic
behaviour, 3D reconstruction in computer graphics
(for example, hierarchical RBF
).
The sum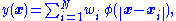
can also be interpreted as a rather simple single-layer type of artificial neural network
called a radial basis function network
, with the radial basis functions taking on the role of the activation functions of the network. It can be shown that any continuous function on a compact
interval can in principle be interpolated with arbitrary accuracy by a sum of this form, if a sufficiently large number N of radial basis functions is used.
The approximant y(x) is differentiable with respect to the weights wi. The weights could thus be learned using any of the standard iterative methods for neural networks.
Using radial basis functions in this manner yields a reasonable interpolation approach provided that the fitting set has been chosen such that is covers the entire range systematically (equidistant data points are ideal). However, without a polynomial term that is orthogonal to the radial basis functions, estimates outside the fitting set tend to perform poorly.
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, so that
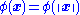; or alternatively on the distance from some other point c, called a center, so that 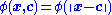. Any function 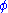that satisfies the property 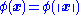is a radial function. The norm is usually Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, although other distance functions are also possible. For example by using Lukaszyk-Karmowski metric
Lukaszyk-Karmowski metric
In mathematics, the Lukaszyk–Karmowski metric is a function defining a distance between two random variables or two random vectors. This function is not a metric as it does not satisfy the identity of indiscernibles condition of the metric, that is for two identical arguments its value is greater...
, it is possible for some radial functions to avoid problems with ill conditioning
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of the matrix solved to determine coefficients wi (see below), since the
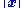is always greater than zero.Sums of radial basis functions are typically used to approximate given functions
Function approximation
The need for function approximations arises in many branches of applied mathematics, and computer science in particular. In general, a function approximation problem asks us to select a function among a well-defined class that closely matches a target function in a task-specific way.One can...
. This approximation process can also be interpreted as a simple kind of neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
.
RBF types
Commonly used types of radial basis functions include (writing):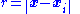
-
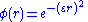
- Multiquadric:
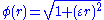
- Inverse Quadratic:
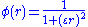
- Inverse Multiquadric:
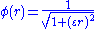
- Polyharmonic splinePolyharmonic splineIn mathematics, polyharmonic splines are used forfunction approximation and data interpolation.They are very useful for interpolation of scattered datain many dimensions.- Definition :Polyharmonic splines are a special case of radial basis functions and...
:
- Polyharmonic spline
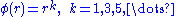
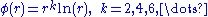
- Thin plate splineThin plate splineThis is a brief derivation for the closed form solutions for smoothing Thin Plate Spline. Details about these splines can be found in ....
(a special polyharmonic spline):
- Thin plate spline
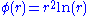
Approximation
Radial basis functions are typically used to build up function approximationFunction approximation
The need for function approximations arises in many branches of applied mathematics, and computer science in particular. In general, a function approximation problem asks us to select a function among a well-defined class that closely matches a target function in a task-specific way.One can...
s of the form
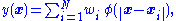
where the approximating function y(x) is represented as a sum of N radial basis functions, each associated with a different center xi, and weighted by an appropriate coefficient wi. The weights wi can be estimated using the matrix methods of linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
, because the approximating function is linear in the weights.
Approximation schemes of this kind have been particularly used in time series prediction and control
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
of nonlinear systems exhibiting sufficiently simple chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
behaviour, 3D reconstruction in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
(for example, hierarchical RBF
Hierarchical RBF
A hierarchical RBF is an interpolation method based on RBF.Interpolation based on RBF used for the construction of shape models in 3D computer graphics , treatment of results from a 3D scanner, terrain reconstruction and others.This problem often named "large scattered data point set...
).
RBF network
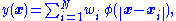
can also be interpreted as a rather simple single-layer type of artificial neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
called a radial basis function network
Radial basis function network
A radial basis function network is an artificial neural network that uses radial basis functions as activation functions. It is a linear combination of radial basis functions...
, with the radial basis functions taking on the role of the activation functions of the network. It can be shown that any continuous function on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
interval can in principle be interpolated with arbitrary accuracy by a sum of this form, if a sufficiently large number N of radial basis functions is used.
The approximant y(x) is differentiable with respect to the weights wi. The weights could thus be learned using any of the standard iterative methods for neural networks.
Using radial basis functions in this manner yields a reasonable interpolation approach provided that the fitting set has been chosen such that is covers the entire range systematically (equidistant data points are ideal). However, without a polynomial term that is orthogonal to the radial basis functions, estimates outside the fitting set tend to perform poorly.