Lukaszyk-Karmowski metric
Encyclopedia
In mathematics
, the Lukaszyk–Karmowski metric is a function
defining a distance
between two random variable
s or two random vectors. This function is not a metric
as it does not satisfy the identity of indiscernibles
condition of the metric, that is for two identical arguments its value is greater than zero.
s X and Y is defined as:
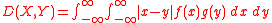
where f(x) and g(y) are the probability density functions of X and Y respectively.
One may easily show that such metrics above do not satisfy the identity of indiscernibles
condition required to be satisfied by the metric
of the metric space
. In fact they satisfy this condition if and only if
both arguments X, Y are certain events described by Dirac delta density probability distribution function
s. In such a case:
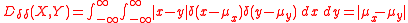
the Lukaszyk-Karmowski metric simply transforms into the metric between expected value
s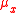
, 
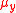of the variables X and Y and obviously:
For all the other cases however:
The Lukaszyk–Karmowski metric satisfies the remaining non-negativity and symmetry
conditions of metric
directly from its definition (symmetry of modulus), as well as subadditivity/triangle inequality
condition:
Thus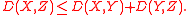
In the case where X and Y are dependent on each other, having a joint probability density function
f(x, y), the L-K metric has the following form:
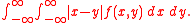
σ, and if moreover X and Y are independent, then D(X, Y) is given by
where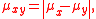
where erfc(x) is the complementary error function
and where the subscripts NN indicate the type of the L-K metric.
In this case, the lowest possible value of the function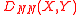
is given by
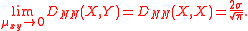
(R) of the same standard deviation
σ, D(X, Y) is given by
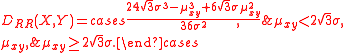
The minimal value of this kind of L–K metric is
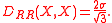
For example for two discrete Poisson-distributed
random variables X and Y the equation above transforms into:
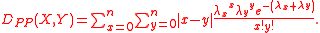
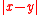with any metric operator d(x,y):
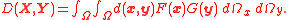
For example substituting d(x,y) with an Euclidean metric and assuming two-dimensionality of random vectors X, Y would yield:
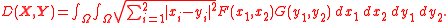
This form of L–K metric is also greater than zero for the same vectors being measured (with the exception of two vectors having Dirac delta coefficients) and satisfies non-negativity and symmetry conditions of metric. The proofs are analogous to the ones provided for the L–K metric of random variables discussed above.
In case random vectors X and Y are dependent on each other, sharing common joint probability distribution F(X, Y) the L–K metric has the form:
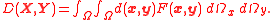
, the Lukaszyk–Karmowski metric for random vectors is defined as:
where:
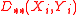
is a particular form of L–K metric of random variables chosen in dependence of the distributions of particular coefficients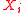
and 
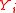of vectors X, Y .
Such a form of L–K metric also shares the common properties of all L–K metrics.
particles described by wavefunction
s ψ, where the probability
dP that given particle is present in given volume of space dV amounts:
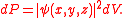
of a quantum particle
(X) in a box
of length L has the form:
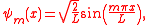
In this case the L–K metric between this particle and any point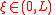
of the box amounts:
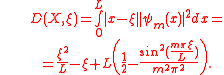
From the properties of the L–K metric it follows that the sum of distances between the edge of the box (ξ = 0 or ξ= L) and any given point and the L–K metric between this point and the particle X is greater than L–K metric between the edge of the box and the particle. E.g. for a quantum particle X at an energy level m = 2 and point ξ = 0.2:
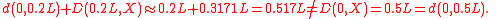
Obviously the L–K metric between the particle and the edge of the box (D(0, X) or D(L, X)) amounts 0.5L and is independent on the particle's energy level.
of length L having time-independent wavefunction
s:
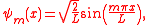
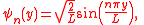
may be defined in terms of Lukaszyk-Karmowski metric of independent
random variables as:
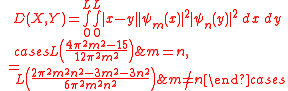
The distance between particles X and Y is minimal for m = 1 i n = 1, that is for the minimum energy levels of these particles and amounts:
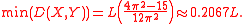
According to properties of this function, the minimum distance is nonzero. For greater energy levels m, n it approaches to L/3.
s, wherein each surveyor of the first group will measure distance between 0 and µx and each surveyor of the second group will measure distance between 0 and µy.
Under the following assumptions we may consider the two sets of received observations xi, yj as random variables X and Y having normal distribution of the same variance σ 2 and distributed over "factual locations" of points µx, µy.
Calculating the arithmetic mean
for all pairs |xi − yj| we should then obtain the value of L–K metric DNN(X, Y). Its characteristic curvilinearity arises from the symmetry of modulus
and overlapping of distributions f(x), g(y) when their means approach each other.
An interesting experiment the results of which coincide with the properties of L-K metric was performed in 1967 by Robert Moyer and Thomas Landauer
who measured the precise time an adult took to decide which of two Arabic digits was the largest. When the two digits were numerically distanced such as 2 and 9. subjects responded quickly and accurately. But their response time slowed by more than 100 milliseconds when they were closer such as 5 and 6, and subjects then erred as often as Once in every ten trials. The distance effect was present both among highly intelligent persons, as well as those who were trained to escape it.
) in various numerical methods, and in particular in approximation algorithms such us radial basis function network
s
, inverse distance weighting
or Kohonen
self-organizing map
s.
This approach is physically based, allowing the real uncertainty in the location of the sample points to be considered.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lukaszyk–Karmowski metric is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defining a distance
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
between two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s or two random vectors. This function is not a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
as it does not satisfy the identity of indiscernibles
Identity of indiscernibles
The identity of indiscernibles is an ontological principle which states that two or more objects or entities are identical if they have all their properties in common. That is, entities x and y are identical if any predicate possessed by x is also possessed by y and vice versa...
condition of the metric, that is for two identical arguments its value is greater than zero.
Continuous random variables
The Lukaszyk–Karmowski metric D between two continuous independent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y is defined as:
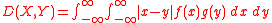
where f(x) and g(y) are the probability density functions of X and Y respectively.
One may easily show that such metrics above do not satisfy the identity of indiscernibles
Identity of indiscernibles
The identity of indiscernibles is an ontological principle which states that two or more objects or entities are identical if they have all their properties in common. That is, entities x and y are identical if any predicate possessed by x is also possessed by y and vice versa...
condition required to be satisfied by the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
of the metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. In fact they satisfy this condition if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
both arguments X, Y are certain events described by Dirac delta density probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
s. In such a case:
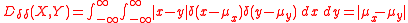
the Lukaszyk-Karmowski metric simply transforms into the metric between expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s
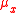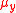, of the variables X and Y and obviously:For all the other cases however:
The Lukaszyk–Karmowski metric satisfies the remaining non-negativity and symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
conditions of metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
directly from its definition (symmetry of modulus), as well as subadditivity/triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
condition:
Thus
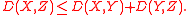
In the case where X and Y are dependent on each other, having a joint probability density function
Joint probability density function
Joint probability density function may refer to:* Probability density function* Joint probability distribution...
f(x, y), the L-K metric has the following form:
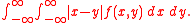
Example: two continuous random variables with normal distributions (NN)
If both random variables X and Y have normal distributions with the same standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
σ, and if moreover X and Y are independent, then D(X, Y) is given by
where
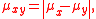
where erfc(x) is the complementary error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
and where the subscripts NN indicate the type of the L-K metric.
In this case, the lowest possible value of the function
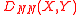is given by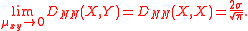Example: two continuous random variables with uniform distributions (RR)
When both random variables X and Y have uniform distributionsUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
(R) of the same standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
σ, D(X, Y) is given by
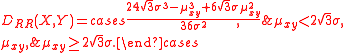
The minimal value of this kind of L–K metric is
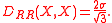
Discrete random variables
In case the random variables X and Y are characterized by discrete probability distribution the Lukaszyk–Karmowski metric D is defined as:For example for two discrete Poisson-distributed
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
random variables X and Y the equation above transforms into:
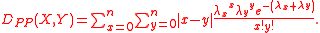
Random vectors
The Lukaszyk–Karmowski metric of random variables may be easily extended into metric D(X, Y) of random vectors X, Y by substituting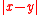 with any metric operator d(x,y):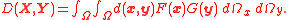For example substituting d(x,y) with an Euclidean metric and assuming two-dimensionality of random vectors X, Y would yield:
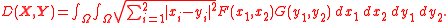
This form of L–K metric is also greater than zero for the same vectors being measured (with the exception of two vectors having Dirac delta coefficients) and satisfies non-negativity and symmetry conditions of metric. The proofs are analogous to the ones provided for the L–K metric of random variables discussed above.
In case random vectors X and Y are dependent on each other, sharing common joint probability distribution F(X, Y) the L–K metric has the form:
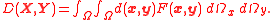
Random vectors – the Euclidean form
If the random vectors X and Y are not also only mutually independent but also all components of each vector are mutually independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, the Lukaszyk–Karmowski metric for random vectors is defined as:
where:
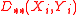
is a particular form of L–K metric of random variables chosen in dependence of the distributions of particular coefficients
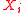and 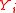of vectors X, Y .Such a form of L–K metric also shares the common properties of all L–K metrics.
- It does not satisfy the identity of indiscernibles condition:
- since:
- but from the properties of L–K metric for random variables it follows that:
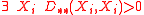
- It is non-negative and symmetric since the particular coefficients are also non-negative and symmetric:
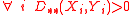
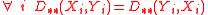
- It satisfies the triangle inequality:
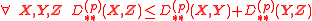
- since (cf. Minkowski inequalityMinkowski inequalityIn mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
):
Physical interpretation
The Lukaszyk–Karmowski metric may be considered as a distance between quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
particles described by wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s ψ, where the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
dP that given particle is present in given volume of space dV amounts:
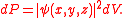
A quantum particle in a box
For example the wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of a quantum particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
(X) in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
of length L has the form:
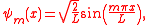
In this case the L–K metric between this particle and any point
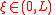of the box amounts: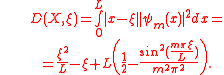From the properties of the L–K metric it follows that the sum of distances between the edge of the box (ξ = 0 or ξ= L) and any given point and the L–K metric between this point and the particle X is greater than L–K metric between the edge of the box and the particle. E.g. for a quantum particle X at an energy level m = 2 and point ξ = 0.2:
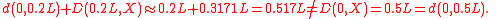
Obviously the L–K metric between the particle and the edge of the box (D(0, X) or D(L, X)) amounts 0.5L and is independent on the particle's energy level.
Two quantum particles in a box
A distance between two particles bouncing in one dimensional boxParticle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
of length L having time-independent wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s:
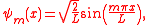
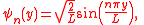
may be defined in terms of Lukaszyk-Karmowski metric of independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables as:
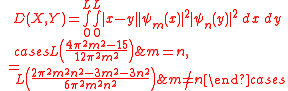
The distance between particles X and Y is minimal for m = 1 i n = 1, that is for the minimum energy levels of these particles and amounts:
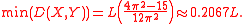
According to properties of this function, the minimum distance is nonzero. For greater energy levels m, n it approaches to L/3.
Popular explanation
Suppose than we have to measure the distance between point µx and point µy, which are collinear with some point 0. Suppose further that we instructed this task to two independent and large groups of surveyors equipped with tape measureTape measure
A tape measure or measuring tape is a flexible form of ruler. It consists of a ribbon of cloth, plastic, fiber glass, or metal strip with linear-measurement markings. It is a common measuring tool. Its flexibility allows for a measure of great length to be easily carried in pocket or toolkit and...
s, wherein each surveyor of the first group will measure distance between 0 and µx and each surveyor of the second group will measure distance between 0 and µy.
Under the following assumptions we may consider the two sets of received observations xi, yj as random variables X and Y having normal distribution of the same variance σ 2 and distributed over "factual locations" of points µx, µy.
Calculating the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
for all pairs |xi − yj| we should then obtain the value of L–K metric DNN(X, Y). Its characteristic curvilinearity arises from the symmetry of modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
and overlapping of distributions f(x), g(y) when their means approach each other.
An interesting experiment the results of which coincide with the properties of L-K metric was performed in 1967 by Robert Moyer and Thomas Landauer
Thomas Landauer
Dr. Thomas K. Landauer is a professor at the Department of Psychology of the University of Colorado.He was one of the pioneers of Latent semantic analysis, and in 1995 published a controversial analysis of the productivity paradox of information technology.He is currently a Vice President at...
who measured the precise time an adult took to decide which of two Arabic digits was the largest. When the two digits were numerically distanced such as 2 and 9. subjects responded quickly and accurately. But their response time slowed by more than 100 milliseconds when they were closer such as 5 and 6, and subjects then erred as often as Once in every ten trials. The distance effect was present both among highly intelligent persons, as well as those who were trained to escape it.
Practical applications
A Lukaszyk–Karmowski metric may be used instead of a metric operator (commonly the Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
) in various numerical methods, and in particular in approximation algorithms such us radial basis function network
Radial basis function network
A radial basis function network is an artificial neural network that uses radial basis functions as activation functions. It is a linear combination of radial basis functions...
s
, inverse distance weighting
Inverse distance weighting
Inverse distance weighting is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points...
or Kohonen
Teuvo Kohonen
Teuvo Kohonen, Dr. Ing , is a Finnish academician and prominent researcher. He is currently professor emeritus of the Academy of Finland.Prof...
self-organizing map
Self-organizing map
A self-organizing map or self-organizing feature map is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional , discretized representation of the input space of the training samples, called a map...
s.
This approach is physically based, allowing the real uncertainty in the location of the sample points to be considered.