Inverse distance weighting
Encyclopedia
Inverse distance weighting (IDW) is a method for multivariate interpolation
, a process of assigning values to unknown points by using values from usually scattered set of known points. Here, the value at the unknown point is a weighted sum of the values of N known points.
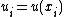for 
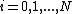using IDW is an interpolating function:
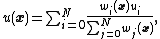
where
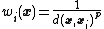
is a simple IDW weighting function, as defined by Shepard, x denotes an interpolated (arbitrary) point, xi is an interpolating (known) point,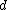
is a given distance (metric
operator) from the known point xi to the unknown point x, N is the total number of known points used in interpolation and
is a positive real number, called the power parameter.
Here weight decreases as distance increases from the interpolated points. Greater values of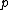
assign greater influence to values closest to the interpolated point. For 0 < p < 1 u(x) has smooth peaks over the interpolated points xi, while as p > 1 the peaks become sharp. The choice of value for p is therefore a function of the degree of smoothing desired in the interpolation, the density and distribution of samples being interpolated, and the maximum distance over which an individual sample is allowed to influence the surrounding ones. For two dimensions, power parameters 
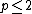, cause the interpolated values to be dominated by points far away, since with a density 
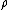of data points and neighboring points between distances 
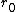to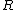 
, the summed weight is approximately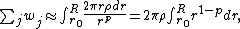
which diverges for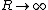
and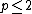 
. For N dimensions, the same argument holds for 
.
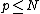Shepard's method is a consequence of minimization of a functional related to a measure of deviations between tuple
s of interpolating points {x, u} and i tuples of interpolated points {xi, ui}, defined as: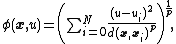
derived from the minimizing condition: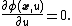
The method can easily be extended to higher dimensional space and it is in fact a generalization of Lagrange
approximation into a multidimensional spaces. A modified version of the algorithm designed for trivariate interpolation was developed by Robert J. Renka and is available in Netlib
as algorithm 661 in the toms library.
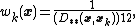
where
is the Lukaszyk-Karmowski metric
chosen also with regard to the statistical error probability distribution
s of measurement of the interpolated points.
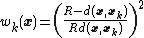
When combined with fast spatial search structure (like kd-tree
) it becomes efficient N*logN interpolation method suitable for large-scale problems.
Multivariate interpolation
In numerical analysis, multivariate interpolation or spatial interpolation is interpolation on functions of more than one variable.The function to be interpolated is known at given points and the interpolation problem consist of yielding values at arbitrary points .-Regular grid:For function...
, a process of assigning values to unknown points by using values from usually scattered set of known points. Here, the value at the unknown point is a weighted sum of the values of N known points.
Shepard's method
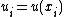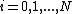A general form of finding an interpolated value u at a given point x based on samples for using IDW is an interpolating function: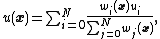where
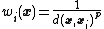
is a simple IDW weighting function, as defined by Shepard, x denotes an interpolated (arbitrary) point, xi is an interpolating (known) point,
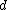is a given distance (metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
operator) from the known point xi to the unknown point x, N is the total number of known points used in interpolation and
is a positive real number, called the power parameter.Here weight decreases as distance increases from the interpolated points. Greater values of
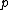assign greater influence to values closest to the interpolated point. For 0 < p < 1 u(x) has smooth peaks over the interpolated points xi, while as p > 1 the peaks become sharp. The choice of value for p is therefore a function of the degree of smoothing desired in the interpolation, the density and distribution of samples being interpolated, and the maximum distance over which an individual sample is allowed to influence the surrounding ones. For two dimensions, power parameters 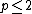, cause the interpolated values to be dominated by points far away, since with a density 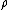of data points and neighboring points between distances 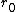to 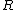, the summed weight is approximately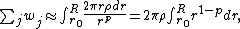which diverges for
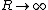and 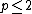. For N dimensions, the same argument holds for 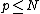.Shepard's method is a consequence of minimization of a functional related to a measure of deviations between tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of interpolating points {x, u} and i tuples of interpolated points {xi, ui}, defined as:
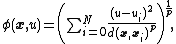
derived from the minimizing condition:
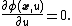
The method can easily be extended to higher dimensional space and it is in fact a generalization of Lagrange
approximation into a multidimensional spaces. A modified version of the algorithm designed for trivariate interpolation was developed by Robert J. Renka and is available in Netlib
Netlib
Netlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
as algorithm 661 in the toms library.
Lukaszyk-Karmowski metric
Yet another modification of the Shepard's method was proposed by Łukaszyk also in applications to experimental mechanics. The proposed weighting function had the form: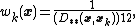where
is the Lukaszyk-Karmowski metricLukaszyk-Karmowski metric
In mathematics, the Lukaszyk–Karmowski metric is a function defining a distance between two random variables or two random vectors. This function is not a metric as it does not satisfy the identity of indiscernibles condition of the metric, that is for two identical arguments its value is greater...
chosen also with regard to the statistical error probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s of measurement of the interpolated points.
Modified Shepard's Method
Another modification of Shepard's method calculates interpolated value using only nearest neighbors within R-sphere (instead of full sample). Weights are slightly modified in this case: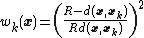When combined with fast spatial search structure (like kd-tree
Kd-tree
In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key...
) it becomes efficient N*logN interpolation method suitable for large-scale problems.