
Thin plate spline
Encyclopedia
This is a brief derivation for the closed form solutions for smoothing Thin Plate Spline. Details about these splines can be found in (Wahba, 1990).
Thin plate splines (TPS) were introduced to geometric design
by Duchon (Duchon, 1976). The name thin plate spline refers to a physical analogy involving the bending of a thin sheet of metal. In the physical setting, the deflection is in the direction, orthogonal to the plane. In order to apply this idea to the problem of coordinate transformation, one interprets the lifting of the plate as a displacement of the
direction, orthogonal to the plane. In order to apply this idea to the problem of coordinate transformation, one interprets the lifting of the plate as a displacement of the  or
or 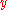 coordinates within the plane. In 2D cases, given a set of
coordinates within the plane. In 2D cases, given a set of  corresponding points, the TPS warp is described by
corresponding points, the TPS warp is described by  parameters which include 6 global affine motion parameters and
parameters which include 6 global affine motion parameters and 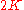 coefficients for correspondences of the control points. These parameters are computed by solving a linear system, in other words, TPS has closed-form solution.
coefficients for correspondences of the control points. These parameters are computed by solving a linear system, in other words, TPS has closed-form solution.
Smoothing TPS is a regularized TPS. The model has a parameter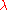 to control how non-rigid is allowed for the deformation.
to control how non-rigid is allowed for the deformation.
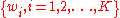 , a radial basis function basically defines a spatial mapping which maps any location
, a radial basis function basically defines a spatial mapping which maps any location  in space to a new location
in space to a new location 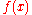 , represented by,
, represented by,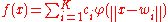
where denotes the usual Euclidean norm
denotes the usual Euclidean norm
and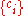 is a set of mapping coefficients.
is a set of mapping coefficients.
One possible choice for the kernel function is the thin plate spline
is the thin plate spline 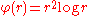 . It has a more global nature than the Gaussian kernel
. It has a more global nature than the Gaussian kernel 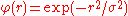 , which is another common function -- a small perturbation of one of the control points always affects the coefficients corresponding to all the other points as well. Note that a thin plate spline is generally understood as a function minimizing the integral of the squared second derivative, typically in two dimensions. This corresponds to the radial basis kernel
, which is another common function -- a small perturbation of one of the control points always affects the coefficients corresponding to all the other points as well. Note that a thin plate spline is generally understood as a function minimizing the integral of the squared second derivative, typically in two dimensions. This corresponds to the radial basis kernel 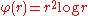 . Other choices of radial basis kernel produce interpolation that would not normally be described as a thin plate spline. For example the Gaussian kernel corresponds to minimization of an infinite sum of derivative terms.
. Other choices of radial basis kernel produce interpolation that would not normally be described as a thin plate spline. For example the Gaussian kernel corresponds to minimization of an infinite sum of derivative terms.
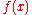 between corresponding point-sets
between corresponding point-sets 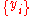 and
and 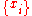 by minimizing the following energy function:
by minimizing the following energy function: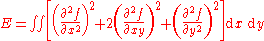
And for a smoothing TPS, it is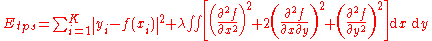
Then smoothing TPS is defined as
For this variational problem, it can be shown that there exists a unique minimizer (Wahba,1990) with a fixed weight parameter
(Wahba,1990) with a fixed weight parameter 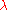 which is presented in the next section. The finite element discretization of this variational problem, the method of elastic maps
which is presented in the next section. The finite element discretization of this variational problem, the method of elastic maps
, is used for data mining
and nonlinear dimensionality reduction
.
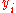 is represented as a vector
is represented as a vector 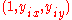 . The unique minimizer
. The unique minimizer  is parameterized by
is parameterized by  which comprises two matrices
which comprises two matrices 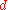 and
and  (
(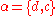 ).
).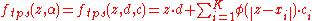
where d is a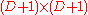 matrix representing the affine transformation and c is a
matrix representing the affine transformation and c is a 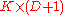 warping coefficient matrix representing the non-affine deformation. The kernel function
warping coefficient matrix representing the non-affine deformation. The kernel function 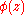 is a
is a 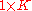 vector for each point
vector for each point  , where each entry
, where each entry 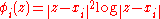 for 2 dimensions. Note that for TPS, the control points
for 2 dimensions. Note that for TPS, the control points 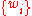 are chosen to be the same as the set of points to be warped
are chosen to be the same as the set of points to be warped 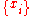 , so we already use
, so we already use 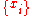 in the place of the control points.
in the place of the control points.
If one substitutes the solution for ,
, 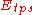 becomes:
becomes: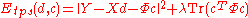
where and
and  are just concatenated versions of the point coordinates
are just concatenated versions of the point coordinates 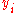 and
and 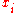 , and
, and 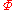 is a
is a 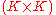 matrix formed from the
matrix formed from the 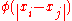 . Each row of each newly formed matrix comes from one of the original vectors. The matrix
. Each row of each newly formed matrix comes from one of the original vectors. The matrix 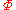 represents the TPS kernel. Loosely speaking, the TPS kernel contains the information about the point-set's internal structural relationships. When it is combined with the warping coefficients
represents the TPS kernel. Loosely speaking, the TPS kernel contains the information about the point-set's internal structural relationships. When it is combined with the warping coefficients  , a non-rigid warping is generated.
, a non-rigid warping is generated.
A nice property of the TPS is that it can always be decomposed into a global affine and a local non-affine component. Consequently, the TPS smoothness term is solely dependent on the non-affine components. This is a desirable property, especially when compared to other splines, since the global pose parameters included in the affine transformation are not penalized.
(Wahba,1990).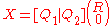
where Q1 and Q2 are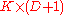 and
and 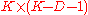 orthonormal matrices, respectively. The matrix
orthonormal matrices, respectively. The matrix  is upper triangular.
is upper triangular.
With the QR decomposition in place, we have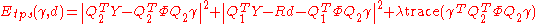
where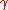 is a
is a 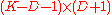 matrix. Setting
matrix. Setting 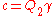 (which in turn implies that
(which in turn implies that 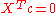 ) enables us to cleanly separate the first term in last third equation into a non-affine term and an affine term (first and second terms last equation respectively).
) enables us to cleanly separate the first term in last third equation into a non-affine term and an affine term (first and second terms last equation respectively).
The least-squares energy function in the last equation can be first minimized w.r.t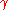 and then w.r.t.
and then w.r.t. 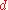 . By applying Tikhonov regularization
. By applying Tikhonov regularization
we have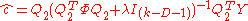
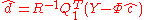
The minimum value of the TPS energy function obtained at the optimum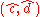 is
is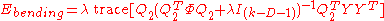
alignment and shape matching.
The popularity of TPS comes from a number of advantages: (1) the interpolation is smooth with derivatives of any order; (2) the model has no free parameters that need manual tuning; (3) it has closed-form solutions for both warping and parameter estimation; and (4) there is a physical explanation for its energy function.
Thin plate splines (TPS) were introduced to geometric design
Geometric design
Geometric design , also known as geometric modelling, is a branch of computational geometry. It deals with the construction and representation of free-form curves, surfaces, or volumes. Core problems are curve and surface modelling and representation...
by Duchon (Duchon, 1976). The name thin plate spline refers to a physical analogy involving the bending of a thin sheet of metal. In the physical setting, the deflection is in the
 direction, orthogonal to the plane. In order to apply this idea to the problem of coordinate transformation, one interprets the lifting of the plate as a displacement of the
direction, orthogonal to the plane. In order to apply this idea to the problem of coordinate transformation, one interprets the lifting of the plate as a displacement of the  or
or  coordinates within the plane. In 2D cases, given a set of
coordinates within the plane. In 2D cases, given a set of  corresponding points, the TPS warp is described by
corresponding points, the TPS warp is described by  parameters which include 6 global affine motion parameters and
parameters which include 6 global affine motion parameters and 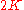 coefficients for correspondences of the control points. These parameters are computed by solving a linear system, in other words, TPS has closed-form solution.
coefficients for correspondences of the control points. These parameters are computed by solving a linear system, in other words, TPS has closed-form solution.Smoothing TPS is a regularized TPS. The model has a parameter
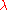 to control how non-rigid is allowed for the deformation.
to control how non-rigid is allowed for the deformation.Radial basis function
Given a set of control points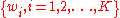 , a radial basis function basically defines a spatial mapping which maps any location
, a radial basis function basically defines a spatial mapping which maps any location  in space to a new location
in space to a new location 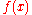 , represented by,
, represented by,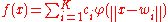
where
 denotes the usual Euclidean norm
denotes the usual Euclidean normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
and
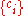 is a set of mapping coefficients.
is a set of mapping coefficients.One possible choice for the kernel function
 is the thin plate spline
is the thin plate spline 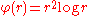 . It has a more global nature than the Gaussian kernel
. It has a more global nature than the Gaussian kernel 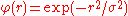 , which is another common function -- a small perturbation of one of the control points always affects the coefficients corresponding to all the other points as well. Note that a thin plate spline is generally understood as a function minimizing the integral of the squared second derivative, typically in two dimensions. This corresponds to the radial basis kernel
, which is another common function -- a small perturbation of one of the control points always affects the coefficients corresponding to all the other points as well. Note that a thin plate spline is generally understood as a function minimizing the integral of the squared second derivative, typically in two dimensions. This corresponds to the radial basis kernel 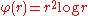 . Other choices of radial basis kernel produce interpolation that would not normally be described as a thin plate spline. For example the Gaussian kernel corresponds to minimization of an infinite sum of derivative terms.
. Other choices of radial basis kernel produce interpolation that would not normally be described as a thin plate spline. For example the Gaussian kernel corresponds to minimization of an infinite sum of derivative terms.Smoothness measure
One of the simplest smoothness measures is the space integral of the square of the second order derivatives of the mapping function. This leads us to the thin plate spline (TPS). The TPS fits a mapping function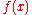 between corresponding point-sets
between corresponding point-sets 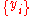 and
and 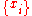 by minimizing the following energy function:
by minimizing the following energy function: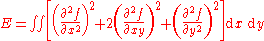
And for a smoothing TPS, it is
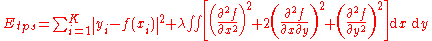
Then smoothing TPS is defined as

For this variational problem, it can be shown that there exists a unique minimizer
 (Wahba,1990) with a fixed weight parameter
(Wahba,1990) with a fixed weight parameter  which is presented in the next section. The finite element discretization of this variational problem, the method of elastic maps
which is presented in the next section. The finite element discretization of this variational problem, the method of elastic mapsElastic map
Elastic maps provide a tool for nonlinear dimensionality reduction. By their construction, they are system of elastic springs embedded in the dataspace. This system approximates a low-dimensional manifold...
, is used for data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
and nonlinear dimensionality reduction
Nonlinear dimensionality reduction
High-dimensional data, meaning data that requires more than two or three dimensions to represent, can be difficult to interpret. One approach to simplification is to assume that the data of interest lies on an embedded non-linear manifold within the higher-dimensional space...
.
Spline
Suppose the points are in 2D (D = 2). One can use homogeneous coordinates for the point-set where a point is represented as a vector
is represented as a vector 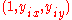 . The unique minimizer
. The unique minimizer  is parameterized by
is parameterized by  which comprises two matrices
which comprises two matrices 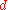 and
and  (
(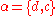 ).
).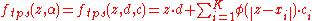
where d is a
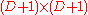 matrix representing the affine transformation and c is a
matrix representing the affine transformation and c is a 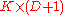 warping coefficient matrix representing the non-affine deformation. The kernel function
warping coefficient matrix representing the non-affine deformation. The kernel function 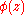 is a
is a 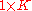 vector for each point
vector for each point  , where each entry
, where each entry 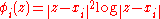 for 2 dimensions. Note that for TPS, the control points
for 2 dimensions. Note that for TPS, the control points 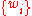 are chosen to be the same as the set of points to be warped
are chosen to be the same as the set of points to be warped 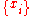 , so we already use
, so we already use 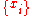 in the place of the control points.
in the place of the control points.If one substitutes the solution for
 ,
, 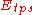 becomes:
becomes: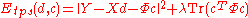
where
 and
and  are just concatenated versions of the point coordinates
are just concatenated versions of the point coordinates 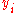 and
and 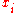 , and
, and 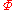 is a
is a 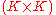 matrix formed from the
matrix formed from the 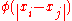 . Each row of each newly formed matrix comes from one of the original vectors. The matrix
. Each row of each newly formed matrix comes from one of the original vectors. The matrix 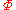 represents the TPS kernel. Loosely speaking, the TPS kernel contains the information about the point-set's internal structural relationships. When it is combined with the warping coefficients
represents the TPS kernel. Loosely speaking, the TPS kernel contains the information about the point-set's internal structural relationships. When it is combined with the warping coefficients  , a non-rigid warping is generated.
, a non-rigid warping is generated.A nice property of the TPS is that it can always be decomposed into a global affine and a local non-affine component. Consequently, the TPS smoothness term is solely dependent on the non-affine components. This is a desirable property, especially when compared to other splines, since the global pose parameters included in the affine transformation are not penalized.
Solution
The separation of the affine and non-affine warping space is done through a QR decompositionQR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
(Wahba,1990).
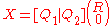
where Q1 and Q2 are
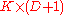 and
and 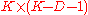 orthonormal matrices, respectively. The matrix
orthonormal matrices, respectively. The matrix  is upper triangular.
is upper triangular.With the QR decomposition in place, we have
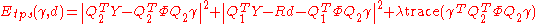
where
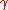 is a
is a 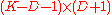 matrix. Setting
matrix. Setting 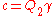 (which in turn implies that
(which in turn implies that 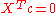 ) enables us to cleanly separate the first term in last third equation into a non-affine term and an affine term (first and second terms last equation respectively).
) enables us to cleanly separate the first term in last third equation into a non-affine term and an affine term (first and second terms last equation respectively).The least-squares energy function in the last equation can be first minimized w.r.t
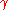 and then w.r.t.
and then w.r.t. 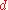 . By applying Tikhonov regularization
. By applying Tikhonov regularizationTikhonov regularization
Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, and, with multiple independent discoveries, it is also variously known as the Tikhonov-Miller method, the...
we have
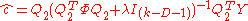
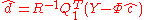
The minimum value of the TPS energy function obtained at the optimum
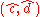 is
is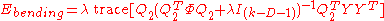
Application
TPS has been widely used as the non-rigid transformation model in imagealignment and shape matching.
The popularity of TPS comes from a number of advantages: (1) the interpolation is smooth with derivatives of any order; (2) the model has no free parameters that need manual tuning; (3) it has closed-form solutions for both warping and parameter estimation; and (4) there is a physical explanation for its energy function.
See also
- Inverse distance weightingInverse distance weightingInverse distance weighting is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points...
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
- Subdivision surfaceSubdivision surfaceA subdivision surface, in the field of 3D computer graphics, is a method of representing a smooth surface via the specification of a coarser piecewise linear polygon mesh...
(emerging alternative to spline-based surfaces) - Elastic mapElastic mapElastic maps provide a tool for nonlinear dimensionality reduction. By their construction, they are system of elastic springs embedded in the dataspace. This system approximates a low-dimensional manifold...
(a discrete version of the thin plate approximation for manifold learning) - SplineSpline (mathematics)In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
- Polyharmonic splinePolyharmonic splineIn mathematics, polyharmonic splines are used forfunction approximation and data interpolation.They are very useful for interpolation of scattered datain many dimensions.- Definition :Polyharmonic splines are a special case of radial basis functions and...
(the thin-plate-spline is a special case of a polyharmonic spline)

