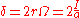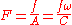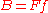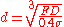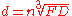Theory of sonics
Encyclopedia
The theory of sonics is a branch of continuum mechanics
which describes the transmission of mechanical energy
through vibration
s. The birth of the theory of sonics can be considered the publication of the book A treatise on transmission of power by vibrations in 1918 by the Romanian
scientist Gogu Constantinescu.
Later on the theory was expanded in electro-sonic, hydro-sonic, sonostereo-sonic and thermo-sonic.
The theory was the first chapter of compressible flow
applications and has stated for the first time the mathematical theory of compressible fluid, and was considered a branch of continuum mechanics
.The laws discovered by Constantinescu, used in sonicity are the same with the laws used in electricity.
The book A treatise on transmission of power by vibrations has the following chapters:
George Constantinescu define his work as follow.

The wavelength λ is =v/n
Assuming that the pipe is finite and closed at the point r situated at a distance which is multiple of λ, and considering that the piston is smaller than wavelength, at r the wave compression is stopped and reflected, the reflected wave traveling back along the pipe.
and
then we have:
Assuming that the fluid current is produced by a piston having a simple harmonic movement, in a piston cylinder having a section Ω.
If we have:
Then:
Where:
If T= period of a complete alternation (one revolution of the crank) then:
The effective current can be defined by the equation:
The stoke volume δ will be given by the relation:
In a pipe were the currents are flowing, we will have:
Considering the above formulas:
If p1 is the pressure at an arbitrary point and p2 pressure in another arbitrary point:
The effective hydromotive force will be: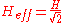
Using experiments R may be calculated from formula:
Where:
If we introduce in the formula, we get:
in the formula, we get:
For pipes with greater diameter greater velocity can be achieve for same value of k.
The loss of power due to friction is calculated with:
The principal function of hydraulic condensers is to counteract inertia effects due to moving masses.
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
which describes the transmission of mechanical energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
through vibration
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s. The birth of the theory of sonics can be considered the publication of the book A treatise on transmission of power by vibrations in 1918 by the Romanian
Romanians
The Romanians are an ethnic group native to Romania, who speak Romanian; they are the majority inhabitants of Romania....
scientist Gogu Constantinescu.
ONE of the fundamental problems of mechanical engineering is that of transmitting energy found in nature, after suitable transformation, to some point at which can be made available for performing useful work. The methods of transmitting power known and practised by engineers are broadly included in two classes: mechanical including hydraulic, pneumatic and wire rope methods; and electrical methods....According to the new system, energy is transmitted from one point to another, which may be at a considerable distance, by means of impressed variations of pressure or tension producing longitudinal vibrations in solid, liquid or gaseous columns. The energy is transmitted by periodic changes of pressure and volume in the longitudinal direction and may be described as wave transmission of power, or mechanical wave transmission. – Gogu Constantinecu
Later on the theory was expanded in electro-sonic, hydro-sonic, sonostereo-sonic and thermo-sonic.
The theory was the first chapter of compressible flow
Compressible flow
Compressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...
applications and has stated for the first time the mathematical theory of compressible fluid, and was considered a branch of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
.The laws discovered by Constantinescu, used in sonicity are the same with the laws used in electricity.
The book A treatise on transmission of power by vibrations has the following chapters:
- Introductory
- Elementary physical principles
- Definitions
- Effects of capacityCapacitorA capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
, inertiaInertiaInertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
, frictionFrictionFriction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, and leakage on alternating currents - Waves in long pipes
- Alternating in long pipes allowing for Friction
- Theory of displacements – motors
- Theory of resonatorResonatorA resonator is a device or system that exhibits resonance or resonant behavior, that is, it naturally oscillates at some frequencies, called its resonant frequencies, with greater amplitude than at others. The oscillations in a resonator can be either electromagnetic or mechanical...
s - High-frequency currents
- Charged lines
- TransformerTransformerA transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
s
George Constantinescu define his work as follow.
Theory of sonics: applications

- CC Gear an interrupter gearInterrupter gearAn interrupter gear is a device used on military aircraft and warships in order to allow them to target opponents without damaging themselves....
device used on military aircraft in order to allow them to target opponents without damaging themselves. - Automatic gear
- Sonic Drilling, was one of the first applications developed by Constantinescu.A sonic drill head works by sending high frequency resonant vibrations down the drill string to the drill bit, while the operator controls these frequencies to suit the specific conditions of the soil/rock geology.
- Torque ConverterTorque converterIn modern usage, a torque converter is generally a type of hydrodynamic fluid coupling that is used to transfer rotating power from a prime mover, such as an internal combustion engine or electric motor, to a rotating driven load...
. A mechanical application of sonic theory on the transmission of power by vibrations. Power is transmitted from the engine to the output shaft through a system of oscillating levers and inertias. - Sonic Engine
Elementary physical principles
If v is the velocity of which waves travel along the pipe, and n the number of the revolutions of the crank aThe wavelength λ is =v/n
Assuming that the pipe is finite and closed at the point r situated at a distance which is multiple of λ, and considering that the piston is smaller than wavelength, at r the wave compression is stopped and reflected, the reflected wave traveling back along the pipe.
| Elementary physical principles | Description |
|---|
| Suppose the crank a to be rotating uniformly, causing the piston b to reciprocate in the pipe c, which is full of liquid. At each in stroke of the piston a zone of high pressure is formed, and these zones, shown by shading, travel along the pipe away from the piston; between every pair of high pressures zones is a zone of light pressure shown in the picture. The pressure at any point in the pipe will go through a series of values from a maximum to a minimum. |
| Assuming that the pipe is finite and closed at the point r situated at a distance which is multiple of λ, and considering that the piston is smaller than the wavelength, at r the wave compression is stopped and reflected, the reflected wave traveling back along the pipe.If the crank continues rotation at uniform speed, a zone of maximum pressure will start from the piston at the same time the reflected wave cme to the piston, as a result the maximum pressure will double. At next rotation the amplitude is increased, and so on, till the pipe burst. |
If instead of a closing pipe we have a piston at r;the wave will be similar at piston b and piston m,the piston m therefore will have the same energy as the piston b; if the distance between the b and m is not a multiple of λ the movement of m will differ in phase compared with the piston b. |
| If more energy is produced by piston b then is taken by piston m the energy will be reflected by piston m in pipe, and the energy will accumulate till the pipe burst.If we have a large volume vessel d, compared with the stroke volume of piston b, the capacity d will act as a spring taking out the energy of direct or reflected waves at high pressure, and giving back energy when pressure fall. The mean pressure in d and in the pipe will be the same. The result of reflected waves will be a stationary wave in pipe with no increase of energy, and the pressure in the pipe will never exceed the pressure limit. |
Waves are transmitted by reciprocating piston along the pipe eeee, the pipe is closed at p at a distance of one complete wavelength. There are branches at one half, three quarter and one full wave length distances. If the p is open and d is open, the motor l will rotate synchronous with motor a. If all valves are closed, there will be a stationary wave with extreme values at λ and λ/2in point b and d, points where the flow will be zero, and where the pressure will alternate between maximum and minimum values determined by the capacity of reservoir f. the maximum and minimum point no not move along the pipe,and no energy flow from generator a. If valve b is open, the motor m is able to take the energy from the line the stationary half wave between a and b being replaced by a traveling wave, still between b and p the stationary wave will persist. If only valve c is open, since at this point the variation of pressure is always zero no energy can be taken out by the motor n, and the stationary wave will persist. If the motor is connected in an intermediary point part of the energy will be taken out by the motor while the stationary wave will persist at reduced amplitude. If the motor l is not capable of consuming all the energy of the generator a, then there will be a traveling wave a and a stationary wave, so there will be no point in the pipe where the pressure variation will be zero, consequently a motor connected at any point of the pipe will be able to use a portion of generated energy. |
Alternating fluid currents
Considering any flow or pipes,if:-
- ω = the area section of the pipe measured in square centimeters;
- v =the velocity of the fluid at any moment in centimeters per second;
and
-
- i =the flow of liquid in square cubic centimeters per seconds,
then we have:
-
- i =vω
Assuming that the fluid current is produced by a piston having a simple harmonic movement, in a piston cylinder having a section Ω.
If we have:
-
- r =the equivalent of driving crank in centimeters
- a =the angular velocity of the crank or the pulsations in radians degree per second.
- n =the number of crank rotations per second.
Then:
-
- The flow from the cylinder to the pipe is: i = I sin(at+φ)
Where:
-
- I = raΩ (the maximum alternating flow in square centimeters per second; Amplitude of the flow.
- t = time in seconds
- φ = the angle of the phase
If T= period of a complete alternation (one revolution of the crank) then:
-
- a = 2πn; where n = 1/T
The effective current can be defined by the equation:
-
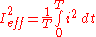 and the effective velocity is :
and the effective velocity is : 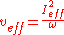
The stoke volume δ will be given by the relation:
Alternating pressures
The alternating pressures are very similar with alternating currents in electricity.In a pipe were the currents are flowing, we will have:
-
 ;where H is the maximum alternating pressure measured in kilograms per square centimeter.
;where H is the maximum alternating pressure measured in kilograms per square centimeter.  the angle of phase;
the angle of phase; 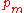 representing the mean pressure in the pipe.
representing the mean pressure in the pipe.
Considering the above formulas:
-
- the minimum pressure is
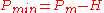 and maximum pressure is
and maximum pressure is 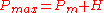
- the minimum pressure is
If p1 is the pressure at an arbitrary point and p2 pressure in another arbitrary point:
-
- The difference
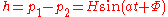 is defined as instantaneous hydromotive force between point p1 and p2, H representing the amplitude.
is defined as instantaneous hydromotive force between point p1 and p2, H representing the amplitude.
- The difference
The effective hydromotive force will be:
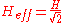
Friction
In alternating current flowing a pipe the friction appear at the surface of the pipe and also in liquid itself. Therefore the relation between the hydromotive and current can be written:-
-
 ; where R= coefficient of friction in
; where R= coefficient of friction in 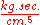
-
Using experiments R may be calculated from formula:
-
-
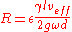 ;
;
-
Where:
-
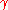 is the density of the liquid in kg per cm.3
is the density of the liquid in kg per cm.3 - l is length of the pipe in cm.
- g gravitational acceleration in cm. per sec.2
-
 section of the pipe in square centimeters.
section of the pipe in square centimeters. - veff the effective velocity
- d internal diameter of the pipe in centimeters.
- for water
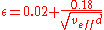 this is an approximation made by experiments.
this is an approximation made by experiments. - h is instantaneous hydromotive force
If we introduce
 in the formula, we get:
in the formula, we get:-
-
 this is equivalent with:
this is equivalent with: -
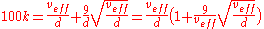 ; introducing k in formula, result thar
; introducing k in formula, result thar 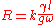
-
For pipes with greater diameter greater velocity can be achieve for same value of k.
The loss of power due to friction is calculated with:
-
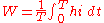 , putting h=Ri result:
, putting h=Ri result: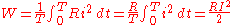
- Therefore:
Capacity and condensers
Definition: Hydraulic condensers are appliances for making alterations in value of fluid currents, pressures or phases of alternating fluid currents. The apparatus usually consists of a mobile solid body, which is dividing the liquid column, and fixed elastically in a middle position, in such way that it follows the movements of the liquid column.The principal function of hydraulic condensers is to counteract inertia effects due to moving masses.
| Hydraulic Condenser Drawing | Theory |
|---|---|
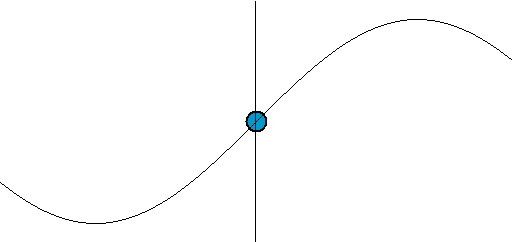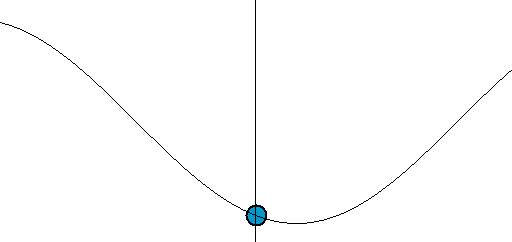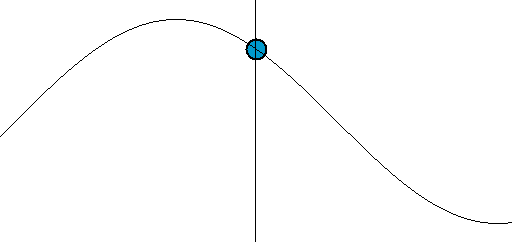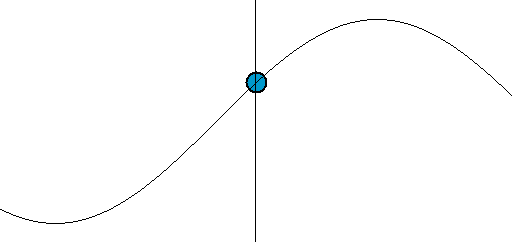 The capacity C of a condenser consisting of a piston of section ω on which the liquid pressure is acting, held in mean position by means of springs, is given by the equation:
where:
and
If the piston is held by a spring at any given moment:
and
In the condenser we will have:
and
Considering the above equations:
and For a spring wire of circular section: Where
and
Therefore:
m being a constant depending on σ and G. If d is the diameter of the spring wire and the D the mean diameter of the spring. Then: so that: if we consider :: 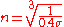 then: then:The above equations are used in order to calculate the springs required for a condenser of a given capacity required to work at a given maximum stress. |