
Thermal de Broglie wavelength
Encyclopedia
In physics
, the thermal de Broglie wavelength is defined for a free ideal gas
of massive particles in equilibrium as
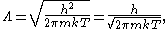
where h is the Planck constant
, m is the mass
of a gas particle, k is the Boltzmann constant, and T is the temperature
of the gas.
The thermal de Broglie wavelength is roughly the average de Broglie wavelength of the gas particles in an ideal gas at the specified temperature. We can take the average interparticle spacing
in the gas to be approximately (V/N)1/3 where V is the volume and N is the number of particles. When the thermal de Broglie wavelength is much smaller than the interparticle distance, the gas can be considered to be a classical or Maxwell–Boltzmann
gas. On the other hand, when the thermal de Broglie wavelength is on the order of or larger than the interparticle distance, quantum effects will dominate and the gas must be treated as a Fermi gas
or a Bose gas
, depending on the nature of the gas particles. The critical temperature is the transition point between these two regimes, and at this critical temperature, the thermal wavelength will be approximately equal to the interparticle distance. That is, the quantum nature of the gas will be evident for
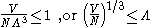
i.e., when the interparticle distance is less than the thermal de Broglie wavelength;
in this case the gas will obey Bose–Einstein statistics
or Fermi–Dirac statistics,
whichever is appropriate. On the other hand, for

i.e., when the interparticle distance is much larger than the thermal de Broglie wavelength,
the gas will obey Maxwell–Boltzmann statistics
.

where c is the speed of light. As with the thermal wavelength for massive particles, this is of the order of the average wavelength of the particles in the gas and defines a critical point at which quantum effects begin to dominate. For example, when the thermal wavelength of the photons in a black body
radiator is of the same order as the wavelength of the radiation (or larger), the "classical" Rayleigh–Jeans law becomes inapplicable, and the "quantum" Planck's law
must be used.
The massless thermal wavelength is derived from the more general definition of the thermal wavelength due to Yan (Yan 2000) described below.
any number of dimensions and for a generalized relationship between energy and
momentum (dispersion relationship) has been given by Yan (Yan 2000). It is of practical importance, since there are many experimental situations with different dimensionality and dispersion relationships. If n is the number of dimensions, and the relationship
between energy (E) and momentum (p) is given by:
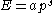
where a and s are constants, then the thermal wavelength is defined as:

where Γ is the Gamma function
. For example, in the usual case of massive
particles in a 3-D gas we have n=3 , and E = p2/2m which gives
the above results for massive particles. For massless particles in a 3-D gas,
we have n=3 , and E=pc which gives the above results for massless particles.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the thermal de Broglie wavelength is defined for a free ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
of massive particles in equilibrium as
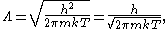
where h is the Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, m is the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of a gas particle, k is the Boltzmann constant, and T is the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of the gas.
The thermal de Broglie wavelength is roughly the average de Broglie wavelength of the gas particles in an ideal gas at the specified temperature. We can take the average interparticle spacing
Mean inter-particle distance
Mean inter-particle distance is the mean distance between microscopic particles in a macroscopic body.-Ambiguity:...
in the gas to be approximately (V/N)1/3 where V is the volume and N is the number of particles. When the thermal de Broglie wavelength is much smaller than the interparticle distance, the gas can be considered to be a classical or Maxwell–Boltzmann
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
gas. On the other hand, when the thermal de Broglie wavelength is on the order of or larger than the interparticle distance, quantum effects will dominate and the gas must be treated as a Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
or a Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
, depending on the nature of the gas particles. The critical temperature is the transition point between these two regimes, and at this critical temperature, the thermal wavelength will be approximately equal to the interparticle distance. That is, the quantum nature of the gas will be evident for
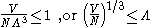
i.e., when the interparticle distance is less than the thermal de Broglie wavelength;
in this case the gas will obey Bose–Einstein statistics
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
or Fermi–Dirac statistics,
whichever is appropriate. On the other hand, for

i.e., when the interparticle distance is much larger than the thermal de Broglie wavelength,
the gas will obey Maxwell–Boltzmann statistics
Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the statistical distribution of material particles over various energy states in thermal equilibrium, when the temperature is high enough and density is low enough to render quantum effects negligible.The expected number of particles...
.
Massless particles
For a massless particle, the thermal wavelength may be defined as:
where c is the speed of light. As with the thermal wavelength for massive particles, this is of the order of the average wavelength of the particles in the gas and defines a critical point at which quantum effects begin to dominate. For example, when the thermal wavelength of the photons in a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
radiator is of the same order as the wavelength of the radiation (or larger), the "classical" Rayleigh–Jeans law becomes inapplicable, and the "quantum" Planck's law
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
must be used.
The massless thermal wavelength is derived from the more general definition of the thermal wavelength due to Yan (Yan 2000) described below.
General definition of the thermal wavelength
A general definition of the thermal wavelength for an ideal quantum gas inany number of dimensions and for a generalized relationship between energy and
momentum (dispersion relationship) has been given by Yan (Yan 2000). It is of practical importance, since there are many experimental situations with different dimensionality and dispersion relationships. If n is the number of dimensions, and the relationship
between energy (E) and momentum (p) is given by:
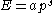
where a and s are constants, then the thermal wavelength is defined as:

where Γ is the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. For example, in the usual case of massive
particles in a 3-D gas we have n=3 , and E = p2/2m which gives
the above results for massive particles. For massless particles in a 3-D gas,
we have n=3 , and E=pc which gives the above results for massless particles.

