Thom conjecture
Encyclopedia
In mathematics
, a smooth algebraic curve
in the complex projective plane, of degree 
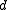, has genus given by the formula
.
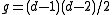The Thom conjecture, named after French mathematician René Thom
, states that if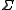
is any smoothly embedded connected curve representing the same class in homology
as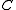
, then the genus 
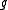of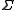 
satisfies
.
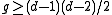In particular, C is known as a genus minimizing representative of its homology class. There are proofs for this conjecture in certain cases such as when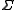
has nonnegative self intersection number
, and assuming this number is nonnegative, this generalizes to Kähler manifold
s (an example being the complex projective plane). It was first proved by Kronheimer
–Mrowka
and Morgan
–Szabó
–Taubes
in October 1994, using the then-new Seiberg–Witten invariant
s.
There is at least one generalization of this conjecture, known as the symplectic Thom conjecture (which is now a theorem, as proved for example by Ozsváth
and Szabó in 2000). It states that a symplectic surface of a symplectic 4-manifold is genus minimizing within its homology class. This would imply the previous result because algebraic curves (complex dimension 1, real dimension 2) are symplectic surfaces within the complex projective plane, which is a symplectic 4-manifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a smooth algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
in the complex projective plane, of degree 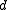, has genus given by the formula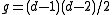.The Thom conjecture, named after French mathematician René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
, states that if
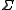is any smoothly embedded connected curve representing the same class in homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
as
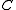, then the genus 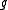of 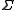satisfies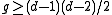.In particular, C is known as a genus minimizing representative of its homology class. There are proofs for this conjecture in certain cases such as when
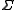has nonnegative self intersection numberIntersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
, and assuming this number is nonnegative, this generalizes to Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s (an example being the complex projective plane). It was first proved by Kronheimer
Peter B. Kronheimer
Peter Benedict Kronheimer is a British mathematician, known for his work on gauge theory and its applications to 3- and 4-dimensional topology. He is presently William Casper Graustein Professor of Mathematics at Harvard University....
–Mrowka
Tomasz Mrowka
Tomasz Mrowka is a Polish American mathematician. He has been the Singer Professor of Mathematics at Massachusetts Institute of Technology since 2010. A graduate of MIT, he received the Ph.D. from University of California, Berkeley in 1988 under the direction of Clifford Taubes and Robion Kirby...
and Morgan
John Morgan (mathematician)
John Willard Morgan is an American mathematician, well known for his contributions to topology and geometry. He is currently the director of the Simons Center for Geometry and Physics at Stony Brook University.-Life:...
–Szabó
Zoltán Szabó
Zoltán Szabó is a professor of mathematics at Princeton University. He created, along with Peter Ozsváth, Heegaard Floer homology, a homology theory for 3-manifolds. For this contribution to the field of topology, Ozsváth and Szabó were awarded the 2007 Oswald Veblen Prize in Geometry.He got his...
–Taubes
Clifford Taubes
Clifford Henry Taubes is the William Petschek Professor of Mathematics at Harvard University and works in gauge field theory, differential geometry, and low-dimensional topology.-Early career:Taubes received his Ph.D...
in October 1994, using the then-new Seiberg–Witten invariant
Seiberg–Witten invariant
In mathematics, Seiberg–Witten invariants are invariants of compact smooth 4-manifolds introduced by , using the Seiberg–Witten theory studied by during their investigations of Seiberg–Witten gauge theory....
s.
There is at least one generalization of this conjecture, known as the symplectic Thom conjecture (which is now a theorem, as proved for example by Ozsváth
Peter Ozsváth
Peter Steven Ozsváth is a professor of mathematics at Princeton University. He created, along with Zoltán Szabó, Heegaard Floer homology, a homology theory for 3-manifolds....
and Szabó in 2000). It states that a symplectic surface of a symplectic 4-manifold is genus minimizing within its homology class. This would imply the previous result because algebraic curves (complex dimension 1, real dimension 2) are symplectic surfaces within the complex projective plane, which is a symplectic 4-manifold.