Thomas-Fermi model
Encyclopedia
The Thomas–Fermi model, named after Llewellyn Thomas
and Enrico Fermi
, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation
. It stands separate from wave function theory as being formulated in terms of the electronic density
alone and as such is viewed as a precursor to modern density functional theory
. The TF model is correct only in the limit of an infinite nuclear charge. Using the approximation for realistic systems yields poor quantitative predictions, even failing to reproduce some general features of the density such as shell structure in atoms and Friedel oscillations in solids. It has, however, found modern applications in many fields through the ability to extract qualitative trends analytically and with the ease at which the model can be solved. The kinetic energy expression of Thomas-Fermi theory is also used as a component in more sophisticated density approximation to the kinetic energy within modern orbital-free density functional theory
.
Working independently, Thomas and Fermi used this statistical model in 1927 to approximate the distribution of electrons in an atom. Although electrons are distributed nonuniformly in an atom, an approximation was made that the electrons are distributed uniformly in each small volume element ΔV (i.e. locally) but the electron density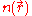
can still vary from one small volume element to the next.
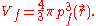
where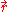
is a point in ΔV.
The corresponding phase space
volume is
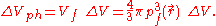
The electrons in ΔVph are distributed uniformly with two electrons per h3 of this phase space volume, where h is Planck's constant. Then the number of electrons in ΔVph is
The number of electrons in ΔV is
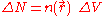
where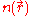
is the electron density.
Equating the number of electrons in ΔV to that in ΔVph gives,
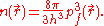
The fraction of electrons at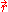
that have momentum between p and p+dp is,
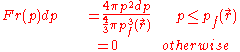
Using the classical expression for the kinetic energy of an electron with mass me, the kinetic energy per unit volume at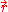
for the electrons of the atom is,
where a previous expression relating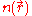
to 
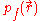has been used and,
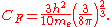
Integrating the kinetic energy per unit volume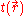
over all space, results in the total kinetic energy of the electrons,
This result shows that the total kinetic energy of the electrons can be expressed in terms of only the spatially-varying electron density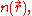
according to the Thomas–Fermi model. As such, they were able to calculate the energy
of an atom using this expression for the kinetic energy combined with the classical expressions for the nuclear-electron and electron-electron interactions (which can both also be represented in terms of the electron density).
is,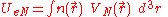
where
is the potential energy of an electron at 
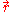that is due to the electric field of the nucleus.
For the case of a nucleus centered at
with charge Ze, where Z is a positive integer and e is the elementary charge
,
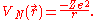
The potential energy of the electrons due to their mutual electric repulsion is,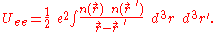
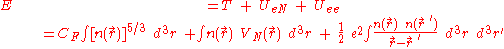
in 1928.
However, the Thomas-Fermi-Dirac theory remained rather inaccurate for most applications. The largest source of error was in the representation of the kinetic energy, followed by the errors in the exchange energy, and due to the complete neglect of electron correlation.
In 1962, Edward Teller
showed that Thomas-Fermi theory cannot describe molecular bonding – the energy of any molecule calculated with TF theory is higher than the sum of the energies of the constituent atoms. More generally, the total energy of a molecule decreases when the bond lengths are uniformly increased. This can be overcome by improving the expression for the kinetic energy.
The Thomas-Fermi kinetic energy can be improved by adding to it the Weizsäcker
(1935) correction:
Llewellyn Thomas
Llewellyn Hilleth Thomas was a British physicist and applied mathematician. He is best known for his contributions to atomic physics, in particular:...
and Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. It stands separate from wave function theory as being formulated in terms of the electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
alone and as such is viewed as a precursor to modern density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
. The TF model is correct only in the limit of an infinite nuclear charge. Using the approximation for realistic systems yields poor quantitative predictions, even failing to reproduce some general features of the density such as shell structure in atoms and Friedel oscillations in solids. It has, however, found modern applications in many fields through the ability to extract qualitative trends analytically and with the ease at which the model can be solved. The kinetic energy expression of Thomas-Fermi theory is also used as a component in more sophisticated density approximation to the kinetic energy within modern orbital-free density functional theory
Orbital-free density functional theory
In computational chemistry, orbital-free density functional theory is a quantum mechanical approach to electronic structure determination which is based on functionals of the electronic density. It is most closely related to the Thomas–Fermi model...
.
Working independently, Thomas and Fermi used this statistical model in 1927 to approximate the distribution of electrons in an atom. Although electrons are distributed nonuniformly in an atom, an approximation was made that the electrons are distributed uniformly in each small volume element ΔV (i.e. locally) but the electron density
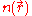can still vary from one small volume element to the next.Kinetic energy
For a small volume element ΔV, and for the atom in its ground state, we can fill out a spherical momentum space volume Vf up to the Fermi momentum pf , and thus,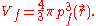where
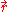is a point in ΔV.The corresponding phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
volume is
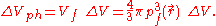
The electrons in ΔVph are distributed uniformly with two electrons per h3 of this phase space volume, where h is Planck's constant. Then the number of electrons in ΔVph is
The number of electrons in ΔV is
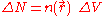
where
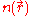is the electron density.Equating the number of electrons in ΔV to that in ΔVph gives,
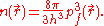
The fraction of electrons at
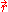that have momentum between p and p+dp is,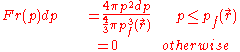Using the classical expression for the kinetic energy of an electron with mass me, the kinetic energy per unit volume at
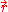for the electrons of the atom is,where a previous expression relating
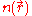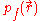to has been used and,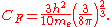Integrating the kinetic energy per unit volume
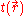over all space, results in the total kinetic energy of the electrons,This result shows that the total kinetic energy of the electrons can be expressed in terms of only the spatially-varying electron density
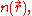according to the Thomas–Fermi model. As such, they were able to calculate the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of an atom using this expression for the kinetic energy combined with the classical expressions for the nuclear-electron and electron-electron interactions (which can both also be represented in terms of the electron density).
Potential energies
The potential energy of an atom's electrons, due to the electric attraction of the positively charged nucleusAtomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
is,
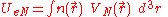
where
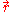is the potential energy of an electron at that is due to the electric field of the nucleus.For the case of a nucleus centered at
with charge Ze, where Z is a positive integer and e is the elementary chargeElementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
,
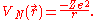
The potential energy of the electrons due to their mutual electric repulsion is,
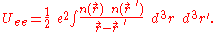
Total energy
The total energy of the electrons is the sum of their kinetic and potential energies,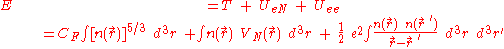Inaccuracies and improvements
Although this was an important first step, the Thomas-Fermi equation's accuracy is limited because the resulting expression for the kinetic energy is only approximate, and because the method does not attempt to represent the exchange energy of an atom as a conclusion of the Pauli principle. A term for the exchange energy was added by DiracPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
in 1928.
However, the Thomas-Fermi-Dirac theory remained rather inaccurate for most applications. The largest source of error was in the representation of the kinetic energy, followed by the errors in the exchange energy, and due to the complete neglect of electron correlation.
In 1962, Edward Teller
Edward Teller
Edward Teller was a Hungarian-American theoretical physicist, known colloquially as "the father of the hydrogen bomb," even though he did not care for the title. Teller made numerous contributions to nuclear and molecular physics, spectroscopy , and surface physics...
showed that Thomas-Fermi theory cannot describe molecular bonding – the energy of any molecule calculated with TF theory is higher than the sum of the energies of the constituent atoms. More generally, the total energy of a molecule decreases when the bond lengths are uniformly increased. This can be overcome by improving the expression for the kinetic energy.
The Thomas-Fermi kinetic energy can be improved by adding to it the Weizsäcker
Carl Friedrich von Weizsäcker
Carl Friedrich Freiherr von Weizsäcker was a German physicist and philosopher. He was the longest-living member of the research team which performed nuclear research in Germany during the Second World War, under Werner Heisenberg's leadership...
(1935) correction:
See also
- Thomas-Fermi approximation for the degeneracy of states