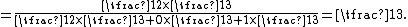Three Prisoners Problem
Encyclopedia
The Three Prisoners problem appeared in Martin Gardner
's Mathematical Games column in Scientific American
in 1959. It is mathematically equivalent to the Monty Hall problem with car and goat replaced with freedom and execution respectively, and also equivalent to, and presumably based on, Bertrand's box paradox
.
The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2, as it is now between him and C. Prisoner A secretly tells C the news, who is also pleased, because he reasons that A still has a chance of 1/3 to be the pardoned one, but his chance has gone up to 2/3. What is the correct answer?
, 
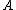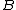and 
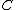the events that the corresponding prisoner will be pardoned, and 
the event that the warden mentions prisoner B as the one not being pardoned, then, using Bayes' formula, the posterior probability of A being pardoned, is:
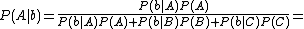
measuring our confidence in their truth in light of all the background information available to us. The problem at hand concerns propositions of the form:
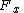: "x will be pardoned", for x equal to one of A, B or C.
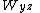: "Replying to y, the warden states that z is executed", for y and z equal to any of A, B or C.
For example,
denotes the proposition "A will be pardoned", and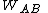 
denotes the proposition "Replying to A, the warden states that B is executed". In this context, "being pardoned" is the complement of "to be executed".
The background information consists of the rules of the game, henceforth denoted by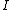
. They impose the following constraints on the probability of such propositions. First, the three prisoners have, a-priori, the same chance of being pardoned, hence the prior probability
of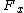
is:
.
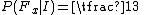Second, the warden is truthful, and will always name as executed a prisoner other than the one questioning him. If he has a choice of two such prisoners, they are equally likely to be named in his response. This rule concerns the conditional probability
of a proposition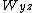
, conditioned on a proposition 
and 
:
Now assume, by renaming the prisoners if necessary, that A is the one questioning the warden, and B the one the warden names as executed. After the warden's reply, As opinion about his chances of being pardoned are expressed by the posterior probability
. Using Bayes' theorem
this is expressed as:
.
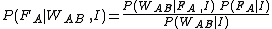By the rules stated above, the numerator of the right-hand side is:
.
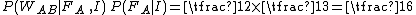The normalizing constant
at the denominator can be evaluated by expanding it using the Law of total probability
:
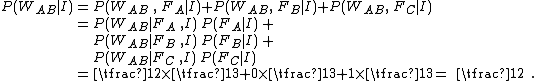
Dividing the numerator by the normalizing constant yields:
.
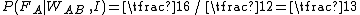As the value of the posterior probability is equal to the prior one, this shows that the warden has given no additional information concerning A 's fate . Further, since B is executed, it is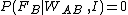
. Hence the chances that C is to be pardoned are, in As opinion,
.
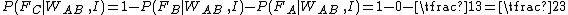Therefore A must judge it safer to try switch his fate with C 's.
With the stipulation that the warden will choose randomly, in the 1/3 of the time that A is to be pardoned, there is a 1/2 chance he will say B and 1/2 chance he will say C. This means that taken overall, 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says B]), the warden will say B because A will be pardoned, and 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says C]) he will say C because A is being pardoned. This adds up to the total of 1/3 of the time (1/6 + 1/6) A is being pardoned, which is accurate.
It is now clear that if the warden answers B to A, cases 1 and 4, which happens 1/2 of the time, 1/3 of the time C is pardoned and A will still be executed (case 4), and only 1/6 of the time A is pardoned (case 1). Hence C's chances are (1/3)/(1/2)=2/3 and A's are (1/6)/(1/2)=1/3.
The key to this problem is that the warden may not reveal the name of a prisoner who will be pardoned. If we eliminate this requirement, it can demonstrate the original problem in another way. The only change in this example is that prisoner A asks the warden to reveal the fate of one of the other prisoners (not specifying one that will be executed). In this case, the warden flips a coin chooses one of B and C to reveal the fate of. The cases are as follows:
Each scenario has a 1/6 probability. The original Three Prisoners problem can be seen in this light: The warden in that problem still has these six cases, each with a 1/6 probability of occurring. However, the warden in that case may not reveal the fate of a pardoned prisoner. Therefore, in the 1/6 of the time that case 3 occurs, since saying B is not an option, the warden says C instead (making it the same as case 4). Similarly, in case 6, the warden must say B instead of C (the same as case 5). That leaves cases 4 and 5 with 1/3 probability of occurring and leaves us with the same probability as above.
neglects to take into account the query
that the warden was asked. Had the query been:
"Will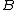
be executed?" then the warden's answer
"Yes,
will be executed" would indeed result
in a probability 1/2 for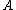
's death. Judea Pearl
(1988) used a variant of this example to demonstrate that
belief updates must depend not merely on the
facts observed but also on the experiment
(i.e., query) that led to those facts.
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
's Mathematical Games column in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
in 1959. It is mathematically equivalent to the Monty Hall problem with car and goat replaced with freedom and execution respectively, and also equivalent to, and presumably based on, Bertrand's box paradox
Bertrand's box paradox
Bertrand's box paradox is a classic paradox of elementary probability theory. It was first posed by Joseph Bertrand in his Calcul des probabilités, published in 1889.There are three boxes:# a box containing two gold coins,...
.
Problem
Three prisoners, A, B and C, are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. The warden knows which one is pardoned, but is not allowed to tell. Prisoner A begs the warden to let him know the identity of one of the others who is going to be executed. "If B is to be pardoned, give me C's name. If C is to be pardoned, give me B's name. And if I'm to be pardoned, flip a coin to decide whether to name B or C."The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2, as it is now between him and C. Prisoner A secretly tells C the news, who is also pleased, because he reasons that A still has a chance of 1/3 to be the pardoned one, but his chance has gone up to 2/3. What is the correct answer?
Solution
The answer is that prisoner A didn't gain information about his own fate. Prisoner A, prior to hearing from the warden, estimates his chances of being pardoned as 1/3, the same as both B and C. As the warden says B will be executed, it's either because C will be pardoned (1/3 chance) or A will be pardoned (1/3 chance) and the B/C coin the warden flipped came up B (1/2 chance; for a total of a 1/6 chance B was named because A will be pardoned). Hence, after hearing that B will be executed, the estimate of A's chance of being pardoned is half that of C. This means his chances of being pardoned, now knowing B isn't, again are 1/3, but C has a 2/3 chance of being pardoned.Mathematical formulation
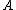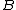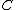Call, and the events that the corresponding prisoner will be pardoned, and the event that the warden mentions prisoner B as the one not being pardoned, then, using Bayes' formula, the posterior probability of A being pardoned, is: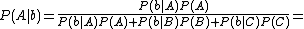
An intuitive explanation
Prisoner A only has a 1/3 chance of pardon. Knowing whether “B” or “C” will be executed does not change his chance. After he hears B will be executed, Prisoner A realizes that if he will not get the pardon himself it must only be going to C. That means there is a 2/3 chance for C to get a pardon.Aids to understanding
As with the Monty Hall Problem, it may be useful to see this problem from alternative viewpoints for better understanding.Bayesian analysis
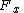An analysis using Bayesian probability theory begins by expressing the problem in terms of statements, or propositions, that may be true or false. Its goal is to compute the probability of these propositions, a number P in measuring our confidence in their truth in light of all the background information available to us. The problem at hand concerns propositions of the form: : "x will be pardoned", for x equal to one of A, B or C. 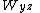: "Replying to y, the warden states that z is executed", for y and z equal to any of A, B or C.For example,
denotes the proposition "A will be pardoned", and 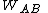denotes the proposition "Replying to A, the warden states that B is executed". In this context, "being pardoned" is the complement of "to be executed".The background information consists of the rules of the game, henceforth denoted by
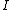. They impose the following constraints on the probability of such propositions. First, the three prisoners have, a-priori, the same chance of being pardoned, hence the prior probabilityPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
of
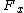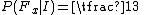is: .Second, the warden is truthful, and will always name as executed a prisoner other than the one questioning him. If he has a choice of two such prisoners, they are equally likely to be named in his response. This rule concerns the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of a proposition
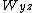, conditioned on a proposition and :-
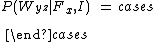
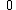
if y = z, (the warden shall not reveal the asking prisoner that he is executed)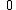 
if z = x, (the warden shall not lie, by indicating as executed a prisoner that, in fact, is to be pardoned)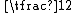 
if y = x, (the prisoner who asks is to be pardoned, and the warden names either one of the others as executed)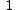 
if y ≠x and y ≠ z, (prisoner z is the only one the warden can mention in reply)
Now assume, by renaming the prisoners if necessary, that A is the one questioning the warden, and B the one the warden names as executed. After the warden's reply, As opinion about his chances of being pardoned are expressed by the posterior probability
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
. Using Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
this is expressed as:
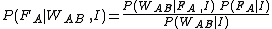.By the rules stated above, the numerator of the right-hand side is:
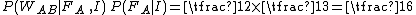.The normalizing constant
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
at the denominator can be evaluated by expanding it using the Law of total probability
Law of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
:
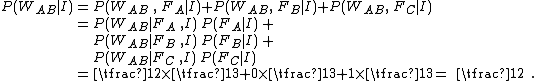
Dividing the numerator by the normalizing constant yields:
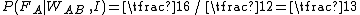.As the value of the posterior probability is equal to the prior one, this shows that the warden has given no additional information concerning A 's fate . Further, since B is executed, it is
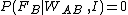. Hence the chances that C is to be pardoned are, in As opinion,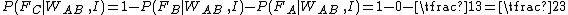.Therefore A must judge it safer to try switch his fate with C 's.
Enumeration of possible cases
The following scenarios may arise:- A is pardoned and the warden mentions B to be executed: 1/3×1/2=1/6 of the cases
- A is pardoned and the warden mentions C to be executed: 1/3×1/2=1/6 of the cases
- B is pardoned and the warden mentions C to be executed: 1/3 of the cases
- C is pardoned and the warden mentions B to be executed: 1/3 of the cases
With the stipulation that the warden will choose randomly, in the 1/3 of the time that A is to be pardoned, there is a 1/2 chance he will say B and 1/2 chance he will say C. This means that taken overall, 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says B]), the warden will say B because A will be pardoned, and 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says C]) he will say C because A is being pardoned. This adds up to the total of 1/3 of the time (1/6 + 1/6) A is being pardoned, which is accurate.
It is now clear that if the warden answers B to A, cases 1 and 4, which happens 1/2 of the time, 1/3 of the time C is pardoned and A will still be executed (case 4), and only 1/6 of the time A is pardoned (case 1). Hence C's chances are (1/3)/(1/2)=2/3 and A's are (1/6)/(1/2)=1/3.
The key to this problem is that the warden may not reveal the name of a prisoner who will be pardoned. If we eliminate this requirement, it can demonstrate the original problem in another way. The only change in this example is that prisoner A asks the warden to reveal the fate of one of the other prisoners (not specifying one that will be executed). In this case, the warden flips a coin chooses one of B and C to reveal the fate of. The cases are as follows:
- A pardoned, warden says: B executed (1/6)
- A pardoned, warden says: C executed (1/6)
- B pardoned, warden says: B pardoned (1/6)
- B pardoned, warden says: C executed (1/6)
- C pardoned, warden says: B executed (1/6)
- C pardoned, warden says: C pardoned (1/6)
Each scenario has a 1/6 probability. The original Three Prisoners problem can be seen in this light: The warden in that problem still has these six cases, each with a 1/6 probability of occurring. However, the warden in that case may not reveal the fate of a pardoned prisoner. Therefore, in the 1/6 of the time that case 3 occurs, since saying B is not an option, the warden says C instead (making it the same as case 4). Similarly, in case 6, the warden must say B instead of C (the same as case 5). That leaves cases 4 and 5 with 1/3 probability of occurring and leaves us with the same probability as above.
Why the paradox?
The tendency of people to provide the answer 1/2neglects to take into account the query
that the warden was asked. Had the query been:
"Will
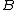be executed?" then the warden's answer"Yes,
will be executed" would indeed resultin a probability 1/2 for
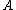's death. Judea PearlJudea Pearl
Judea Pearl is a computer scientist and philosopher, best known for developing the probabilistic approach to artificial intelligence and the development of Bayesian networks ....
(1988) used a variant of this example to demonstrate that
belief updates must depend not merely on the
facts observed but also on the experiment
(i.e., query) that led to those facts.
Related problems and applications
- Principle of restricted choice, an application in the card game bridgeContract bridgeContract bridge, usually known simply as bridge, is a trick-taking card game using a standard deck of 52 playing cards played by four players in two competing partnerships with partners sitting opposite each other around a small table...
- Prisoner's dilemmaPrisoner's dilemmaThe prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
, a game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
problem - Bertrand's box paradoxBertrand's box paradoxBertrand's box paradox is a classic paradox of elementary probability theory. It was first posed by Joseph Bertrand in his Calcul des probabilités, published in 1889.There are three boxes:# a box containing two gold coins,...
(also known as the three-cards problem) - Boy or Girl paradox
- Two envelopes problemTwo envelopes problemThe two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle or paradox in logic, philosophy, probability and recreational mathematics, of special interest in decision theory and for the Bayesian interpretation of probability theory...
- Sleeping Beauty problemSleeping Beauty problemThe Sleeping Beauty problem is a puzzle in probability theory and formal epistemology in which an ideally rational epistemic agent is to be wakened once or twice according to the toss of a coin, and asked her degree of belief for the coin having come up heads....